The main program
The main program sets the sample excitation parameters, the transient acquisition conditions, initiates the measurement, acquires the transient, and finally, converts it into the spectrum. The main program allows to:
- measure the kinetics of the non-stationary process,
- govern the hardware, set up the excitation and acquisition parameters,
- perform preliminary analysis of the time constant(-s), make the noise histogram
- initiate the numerical calculations leading to the Laplace transform inversion,
- send the data and calculation result files to the data base which helps compare, manipulate, analyse and visualise the results,
- personalise all system parameters.
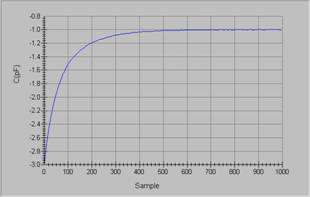
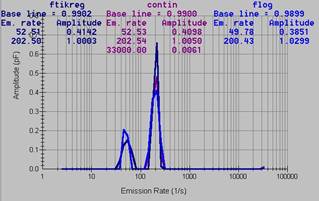 A transient and a spectrum obtained from this transient using three different numerical routines
A transient and a spectrum obtained from this transient using three different numerical routines
[Top]
Numerical routines
A common approach to the quantitative description of non-exponentiality observed in the non-stationary processes is to assume that they are characterized by a spectrum of emission rates, where f(t) is the recorded transient and F(s) is the spectral density 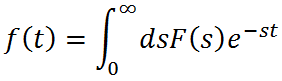 function. A mathematical representation of the capacitance transients given by the equation is the Laplace transform of the true spectral function F(s). Thus, to find a real spectrum of the emission rates (time constants) present in the transient it is necessary to use a mathematical algorithm that effectively performs an inverse Laplace transform for the function f(t). The result of such a procedure is a spectrum of delta-like peaks for multi-, mono-exponential transients or a broad spectrum with no fine structure for continuous distribution. In this method it is not necessary to make any a priori assumptions about the functional shape of the spectrum, except that all decays are exponential in the same direction.
function. A mathematical representation of the capacitance transients given by the equation is the Laplace transform of the true spectral function F(s). Thus, to find a real spectrum of the emission rates (time constants) present in the transient it is necessary to use a mathematical algorithm that effectively performs an inverse Laplace transform for the function f(t). The result of such a procedure is a spectrum of delta-like peaks for multi-, mono-exponential transients or a broad spectrum with no fine structure for continuous distribution. In this method it is not necessary to make any a priori assumptions about the functional shape of the spectrum, except that all decays are exponential in the same direction.
In general, a problem of solving of Fredholm-type integral equations is fundamentally ill posed, thus complex numerical approximation methods have to be used. Among many, the Tikhonov regularization method turned out to be very effective. More details on the Tikhonov method can be found in a short description (20kB) prepared by one of the Copernicus Project partners. The evolution of the Laplace DLTS technique over the last years has enabled us to achieve the theoretical limit of resolution of the DLTS method. For relatively shallow states that emit at low temperature, the reduction in line-width is remarkable and can give us more than two orders of magnitude increase in resolution over Lang's technique. We have devoted much effort to making the technique usable, i.e., establishing stability of the algorithm and improving the hardware so that the theoretical limit is achievable. This is been done under a Copernicus contract. See also a list of the scientific publications prepared during the process of the method development.
In this experimental manifestation of the Laplace DLTS system three different software procedures are used for the numerical calculations. All of them are based on the Tikhonov regularization method, however they differ in the way the criteria for finding the regularization parameters are defined. The first one (CONTIN) [W. Provencher, Comput. Phys. Commun. 27, 213 (1982) (http://dx NULL.doi NULL.org/10 NULL.1016/0010-4655%2882%2990173-4)] is in the public domain and has been obtained from The Computer Physics Communication (CPC) Program Library (http://www NULL.cpc NULL.cs NULL.qub NULL.ac NULL.uk/) at the Queen’s University of Belfast and modified in order to integrate it with our system. The outline code of the second one (FTIKREG) [J. Weese, Comput. Phys. Commun. 69, 99 (1992) (http://dx NULL.doi NULL.org/10 NULL.1016/0010-4655%2892%2990132-I); ibid. 77, 429 (1993) (http://dx NULL.doi NULL.org/10 NULL.1016/0010-4655%2893%2990187-H)] is distributed by the same library but it has been substantially modified by the original authors for operation within this Laplace DLTS system. The last one (FLOG) has been specifically developed for the system [A. Matulis]. The parallel use of three different software packages substantially increases the level of confidence in the spectra obtained. The procedures are used as Dynamically Linked Libraries (DLL), which means that they can exchange data with the main application through the computer memory with no input and output files. Additionally, for preliminary data analysis a discrete (multiexponential) deconvolution method can be used [Z. Kancleris]. This method is based on a simple integration procedure [K. Tittelbach-Helmrich, Meas. Sci. Technol. 4, 1323 (1993) (http://dx NULL.doi NULL.org/10 NULL.1088/0957-0233/4/12/003)].
Non-stationary processes analysis (http://www NULL.iop NULL.org/EJ/abstract/0957-0233/4/12/003/)
In physics and technique there is a number of problems where a similar approach to the data analysis could be employed. For example, in investigations of semiconductor materials one deals with the photoluminescence, photocurrent, or photocapacitance kinetics. In the particle or nuclear physics there are particle or isotopes decaying processes, and finally, in a device technology there is a problem of ageing or degradation of optical or electronic components. Moreover, applying different kernels of the Fredholm-type integral equation one can model a variety of different physical processes. The system software and hardware can be easily modified or adopted in order to meet specific requirements of other possible applications. This led to an idea of building the version of the high-resolution transient processes analyser which is able to use a much broader range of pieces of the hardware.
Additional bibliography
- W.H. Press, S.A. Teukolsky, W.T. Veterling, B.P.Flannery, Numerical recipes in C (Cambridge, University Press, 1995).
- C.L. Lawson, R.J.Hanson, Solving least squares problems (Philadelphia, SIAM, 1995)
- C.W. Groetsch, The theory of Tikhonov regularization for Fredholm equations of the first kind, Pitman, London, 1984.
- J. Honerkamp and J. Weese, Tikhonov's regularisation method for ill posed problems, Continuum Mech. Thermodyn. 2, 17 (1990) (http://dx NULL.doi NULL.org/10 NULL.1007/BF01170953); J. Weese, A reliable and fast method for the solution of Fredholm integral equations of the first kind based on Tikhonon regularization, Computer Physics Communications 69, 99 (1992) (http://dx NULL.doi NULL.org/10 NULL.1016/0010-4655%2892%2990132-I).
[Top]
Experiment Data Base program
The Experimental Data Base is a part of the Laplace Transient Processor system and it is the tool which is central to data manipulation, visualization, and analysis. During the design process we have attempted to meet the specific needs of this experimental technique and also to be compatible with other experiments which may accompany the main system. The principal need was that it should be possible to store and then easily manipulate large amounts of data. The database system runs in the background of the measurement, stores data and all parameters, that describe the measuring process, and the data itself. Afterwards it enables the user to extract, compare, visualize and maintain gathered data.
The Database part of the Laplace Transient Processor system is based on Microsoft Access Jet database engine version 3.5. The database file contains only structure definition (tables and relations), some SQL queries and data itself. Data maintenance, manipulation, reviewing, inspecting and visualization are done from within a separate program. A Visual Basic program contains the entire user interface and data manipulation tools. The program may run as a separate application, without the need to communicate with the measurement system. It can also be run in parallel with measurement program, in which case data loaded into the database during the experiment may be inspected immediately.
From a user’s point of view the data structure is as follows:
material description and data,
└ sample description and data,
└ measurement parameters and file name,
└ computed results file name.
[Top]
Defect Data Base program
This program is a part of the Laplace Transient Processor system is a tool to gather information about defects measured by a user and the ones which have reliable experimental data in the literature. This program is meant to be used solely with the Laplace and conventional DLTS measurements.
[Top]
Test transient generator
This is a stand-alone program which allows a transient to be generated for an assumed spectrum. This process of transient generation is equivalent to the calculation the Laplace transformation for a given spectrum. This application allows a user to perform tests on the numerical methods applied by the main application. One of the functions of this program is to reproduce the transient from a spectrum which has been calculated from the real data. This spectrum can then be used as the basis for an inverse Laplace transform procedure in order to check the system reliability.
[Top]
Transient Processing Utility NEW!
This is a stand-alone program which allows for transient numerical analysis using the same methods as the main Laplace DLTS program.
It may be used as an auxiliary utility to augment analysis of transients already stored in the database, as manipulating numerical routines parameters’ and input data is much more convinient than in the main program. Newly computed spectra may be stored into the database parallel to the existing ones.
The utility may be also used as a separate program to process any suitable data, i.e. exponential transients, stored in text files conforming to the Laplace DLTS System standard (descibed in the TPU help for users’ convinience). TPU may work on text files only (both input and output, also conforming to the standard), but may be used as well in tandem with the experiment database program for storing both input and output data. The ExpDBase program is sold togethr with the Transient Processing Utility; this is the same program as in the main system.
[Top]