kuzminov

Sea-Bottom Profile -- Remote Determination Problem in Geometrical Approach

Second General Education Technical Lyceum attached to Samara State Technical University, Rabochaya 19, 443041 Samara, Russia

In this paper the problem of remote diagnosis and nondestructive investigation of a surrounding medium is discussed. Recently such problems have been assigned to the field of tomography, i.e. investigations of the inner structure of objects. The general principle of this method is as follows: some of the properties are unknown in the course of investigation. It can be for example substance density, vibration propagation velocity and velocity of the transfer of energy, various coefficients describing absorption or dispersion. According to the set of initial information the researcher tries to calculate values of unknown quantities. Solution of such problems consists in the determination of a functional dependence linking all the desired parameters and all the known circumstantial characteristics to the general physical law describing the process which has been established theoretically.

These problems are named inverse ones, as opposed to the primal problems in which all the initial parameters entering into the theoretical law which describes the process are known. In the inverse problems one or a few such parameters are unknown and they are the subject of determination. Hence, the solutions of primal problems model real processes prescribed by all initial characteristics. On the other hand, solutions of inverse ones make it possible to restore some unknown parameters of the real process according to the set of circumstantial experimental data.

Using such an approach the researcher deals not with real physical phenomena but with their more or less adequate mathematical models that present only a numerical image of the real situation. It is clear that in this case computer simulation, size of its resources and possibilities begin to play an important role. This circumstance was the main retarding factor in all such investigation methods for a long time.

The fundamental advantage of tomographic approach is that in the course of data collection the inner structure of the medium being investigated is not disturbed since only the response on the ``soft'' external actions is recorded. Such investigation methods are called nondestructive and remote methods.

The tomographical principles are used in various fields of science: in geophysics -- in the course of searching for ore deposits and oil fields by seismic prospecting methods; in nondestructive testing -- for detecting internal defects of structures and for their localization; for investigation of the atmosphere and the oceans using sound waves; in research and technology -- for real-time control of experimental and technological processes. Shortly speaking, tomography is used everywhere where there is a need for nondestructive controlling and remote diagnosis.

Now let us consider an example of the simplest problem arising, for instance, in the course of determination of a sea-bottom profile in oceanography. It is clear that it would be difficult to conduct such investigations directly by plunging a lead-and-line into a water at great depths and measuring its length, that is, directly penetrating the internal structure of the ocean. In this case it is more preferable to conduct remote measurements with the help of echo ranging principles.

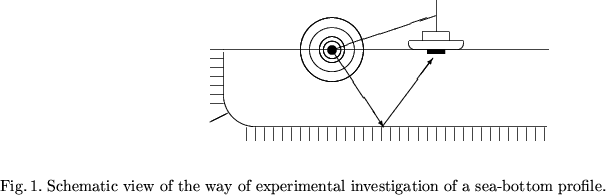
Let us organize an observation system in the following manner: let us place a source of an audio signal on a floating buoy attached to a ship by a halyard. A signal receiver is located aboard the ship as shown in Fig. 1.

$\begin{figure}\centering\begin{picture}(100,40)(-13,0)\put(86.5,26.5){\oval(143,... ...w of the way of experimental investigation of a sea-bottom profile.}\end{figure}$

Let us suppose that the source has a power of P₀, and at the time T₀ the source emits an isotropic signal during a small time interval $\Delta T^ *$ . Let us also suppose that the propagation velocity of this signal in the water is constant and is equal to some known value c₀. At the time T₁>T₀ the front of the sound wave will be a semisphere of the radius r( T₁)=c₀(T₁-T₀) with the centre at the source. We make an assumption that the sound waves propagate along straight lines in agreement with the laws of geometrical acoustics.

Let us assume also that a considerable energy absorption takes place on the water surface and thus there are practically no reflection effects from it, but energy losses are negligibly small in the water. In addition to this fact let us assume that during interaction with the sea bottom the signal loses a part of its energy, the double reflection from the bottom can be ignored.

As pointed out above we assume that the reflection of the signal from the bottom obeys the law of geometrical acoustics, and the signal reflection angle is equal to the angle of its incidence on the sea bottom.

To complete this description let us assume that the attenuation of the signal power depending upon its path length in the water obeys the law

$\begin{displaymath}P(L)=\frac {P_0}2\left(1-\frac L{\sqrt{\epsilon^2+L^2}}\right),\eqno(1)\end{displaymath}$

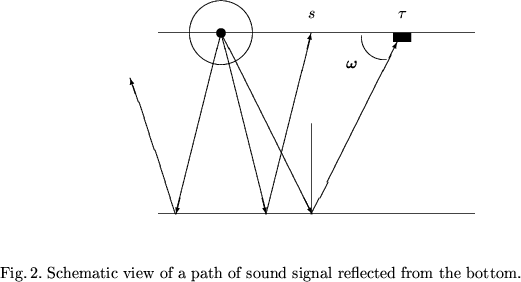
We assume the motion of the ship as linear and uniform with velocity $v_0 \ll c_0$ . Thus, the procedure of data collection is the following: the ship with a sound radiation receiver placed aboard begins a uniform motion along the straight line with the velocity of v₀ at the time T₀, from the point of coordinate x₀. The radiation source placed on the buoy is mounted rigidly to the ship and moves along the same straight line in the same direction and with the same velocity as the ship, but in a distance s from it.

Starting at the time T₀ the source emits short audio signals of time duration $\Delta T^*$ . The radiation proceeds at regular intervals $\Delta T \gg\Delta T^*$ , within which the ship travels the distance $\Delta S=v_0 \Delta T$ . The sound signal travelling through the water reflects from the sea bottom and reaches the receiver which measures its propagation time

$\begin{figure}\centering\begin{picture}(135,57)(-21,0)\put(10,50){\line(1,0){70}... ...Schematic view of a path of sound signal reflected from the bottom.}\end{figure}$

$\begin{figure}\centering\begin{picture}(20,57)(20,0)\put(30,35){\circle {14}}\p... ....9\textwidth}{Fig.\,3.~Schematic view of receiver with collimators.}\end{figure}$

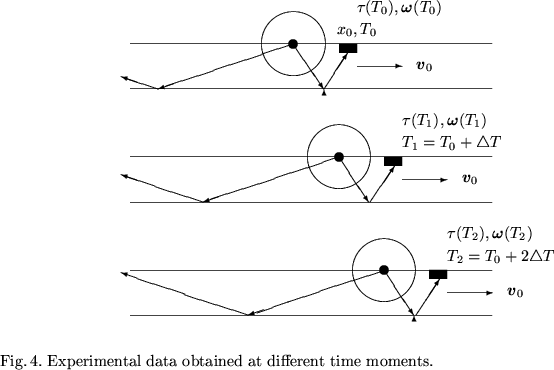
According to our assumption velocity of the signal in the water considerably exceeds the ship velocity. Hence, when the signal comes to the transducer the ship is at the same point as at the moment when the source emitted the signal. After a set of n successive signal emissions at the time moments $T_i=T_0+i\Delta T,~i=1,\ldots,n$ , we will possess a set of experimental data of $\tau(T_i),~\mbox{\boldmath$\omega$}(T_i)$ as shown in Fig. 4.

$\begin{figure}\centering\begin{picture}(95,78)(5,3)\put(10, 10){\line(1,0){80}}... ...dth}{Fig.\,4.~Experimental data obtained at different time moments.}\end{figure}$

Let us consider an interpolation (approximate detecting the sea-bottom profile) according to data $\tau(T_i),~\mbox{\boldmath$\omega$}(T_i),~i=1,\ldots,n$ . We will consider this problem as a two-dimensional one, taking into account vertical cross-section of the ship and the sea bottom, which significantly simplifies the problem.

Now we will perform mathematical modelling of the problem. We will do it in two stages. The first one will consist in modelling the process of experimental data collection and will include setting a sea-bottom profile curve, modelling sound propagation processes through the water and its reflection from the bottom profile, modelling conditions for emitted signals to reach the receiver placed aboard the ship, calculating experimental data $\tau(T_i),~\mbox{\boldmath$\omega$}(T_i)$ . This step will be realized in Sec. 3.

The second stage of our investigation will be the construction of an algorithm for solving a sea-bottom profile interpolation problem according to data on time of propagation of the signal from the radiation source to the radiation receiver $\tau(T_i)$ and on $\mbox{\boldmath$\omega$}(T_i)$ -- the direction vector of the beam which comes to the receiver of the signal. This will be calculated in Sec. 4. It will be shown further that the values of $\tau(T_i), ~\mbox{\boldmath$\omega$}(T_i)$ obtained as a result of one measurement make it possible to determine the radius-vectors of the points of the sea-bottom profile from which the signal was reflected. The combination of the data obtained as a result of n observations make it possible to determine the points which are on the sea-bottom profile and to perform interpolation according to them.

Our final goal is to develop and test a computational algorithm for solving model problems set with the help of package ``Maple-V, Release 3 for Windows".

As a primal problem we understand a problem of collection of experimental data $\tau(T_i),~\mbox{\boldmath$\omega$}(T_i)$ depending upon the sound signal propagation conditions through the water and upon its interaction with the sea-bottom profile. We will assume that the sea-bottom profile is described by a curve in R² lying completely in the fourth quarter of the coordinate plane. Let us suppose that the parameter of this curve is the first component of the radius-vector of the plane point x₁ and let us set $x_1=t\in[0,b)\subseteq R$ . Let us also assume that at t=0 the curve passes through the origin of the coordinates system. In other words

$\begin{displaymath}\mbox{\boldmath $x$}(t)=(t,f(t)),\quad f(0)=0,\quad f(t)\le0,\quad t\in[0,b),\eqno(2)\end{displaymath}$

In such a case the shore zone is known, and on the sea-bottom curve a point with the zero radius and with the vector ${\bf0}=(0,0)$ corresponds to it.

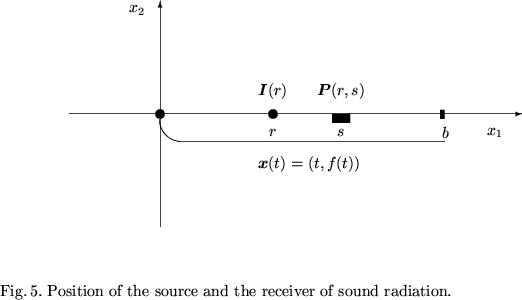
Let us furthermore assume that the source and the receiver of sound radiation are placed at two different points of the straight line 0x₁ at a fixed distance s apart and that their radius-vectors (Fig. 5) have the following coordinates:

$\begin{displaymath}\mbox{\boldmath $I$}(r)=r\mbox{\boldmath $e$}_1=(r,0),\end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $P$}(r,s)=(r+s)\mbox{\boldmath $e$}_1=(r+s,0) ;~r>0,~s>0,~r,r+s\in[0,b),\eqno(3)\end{displaymath}$

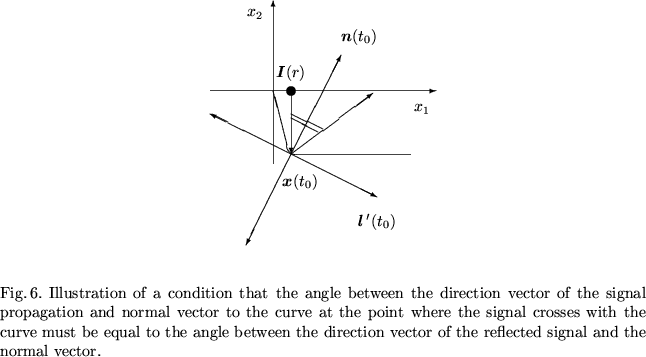
As indicated above we assume that the angle of incidence of the signal on the sea-bottom profile is equal to the angle of reflection. In our case it means that the angle between the direction vector of the signal radiation transfer and the vector tangent to the curve at the point where the signal crosses with the curve is equal to the angle between the direction vector of the reflected signal and the same tangent vector (Fig. 6).

$\begin{figure}\centering\begin{picture}(156,61)(-12, 0)\put(93,35.5){\oval(126,... ...ig.\,5.~Position of the source and the receiver of sound radiation.}\end{figure}$

$\begin{figure}\centering\begin{picture}(20,60)(25,-3)\put (54.5,28.5){\oval(55,... ...he direction vector of the reflected signal and the normal vector.}\end{figure}$

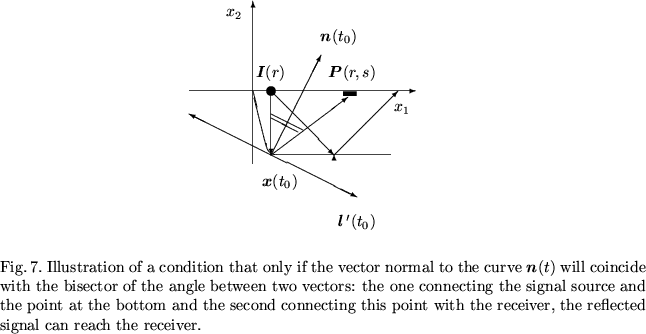
For simulation of the recording process of the signal reflected from the sea bottom it is necessary to determine the coordinates of the radius-vector of the point of curve $\mbox{\boldmath$x$}(t)$ for which the radiation incidence angle from a source on the tangent line at this point is equal to the angle between this tangent line and the straight line connecting this point with the receiver location point. Only under this condition the reflected signal can reach the receiver; otherwise it will not be able to reach it (Fig. 7). From geometrical considerations it is not difficult to write the equation for the radius-vector components of such points.

$\begin{figure}\centering\begin{picture}(85,60)(0,3)\put(57.5,28.5){\oval(55,5) ... ...nt with the receiver, the reflected signal can reach the receiver.}\end{figure}$

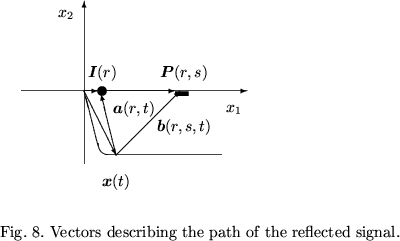
$\begin{figure}\centering\begin{picture}(145,53)(-20,5)\put(30,21){\line(-1,4)3}\... ...re}\par Fig.~8.~Vectors describing the path of the reflected signal.\end{figure}$

$\begin{displaymath}\mbox{\boldmath $I$}(r)=\mbox{\boldmath $a$}(r,t)+\mbox{\bold... ...s)=\mbox{\boldmath $b$}(r,s,t)+\mbox{\boldmath $x$}(t).\eqno(4)\end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $a$}(r,t)=\mbox{\boldmath $I$}(r)-\mbox{\bold... ...s,t)=\mbox{\boldmath $P$}(r,s)-\mbox{\boldmath $x$}(t),\eqno(5)\end{displaymath}$

$\begin{displaymath} \mbox{\boldmath $a$}(r,t)=(r-t,-f(t)),\qquad\mbox{\boldmath $b$}(r,s,t)=(r+s-t,-f(t)).\eqno(6) \end{displaymath}$

Hereafter it will be convenient to use unit vectors pointing these directions, that is, the following vectors:

$\begin{displaymath} \mbox{\boldmath $a$}_0(r,t)=\frac{\mbox{\boldmath $a$}(r,t)}... ... $b$}(r,s,t)}{\Vert\mbox{\boldmath $b$}( r,s,t)\Vert}.\eqno(7)\end{displaymath}$

Let us construct the bisector of the angle $\angle(\mbox{\boldmath$a$}_0(r,t),\mbox{\boldmath$b$}_0(r,s,t ))$ between the vectors $\mbox{\boldmath$a$}_0(r,t)$ and $\mbox{\boldmath$b$}_0(r,s,t)$ . It will be simply equal to the vector sum

$\begin{displaymath}\mbox{\boldmath $a$}_0(r,t)+\mbox{\boldmath $b$}_0(r,s,t)=\mbox{\boldmath $biss$}(r,s,t). \eqno(8)\end{displaymath}$

The signal from the source will come to the receiver after reflection from the sea-bottom profile point with the radius-vector $\mbox{\boldmath$x$}(t_0)$ if at this point the vector $\mbox{\boldmath$biss$}(r,s,t_0)$ is orthogonal to the vector tangent to the sea-bottom profile curve at this point ${\mbox{\boldmath$l$}}\,'(t_0)$ . Under all these assumptions the tangent line vector is defined as

$\begin{displaymath} {\mbox{\boldmath $l$}}\,'(t)=(1,f'(t)). \eqno(9) \end{displaymath}$

Consequently the coordinates of the radius-vector of the points at sea-bottom profile for which the reflected signal will be able to reach the receiver are defined by the equation

$\begin{displaymath} \langle\mbox{\boldmath $biss$}(r,s,t_0),{\mbox{\boldmath $l$}}\,'(t_0)\rangle=0 \eqno(10)\end{displaymath}$

Solving this equation for different values r_i (distances from the source to the shore zone) and for the fixed value s (constant distance from the source to the receiver placed aboard the ship) which characterize their different locations during the ship motion

$\begin{displaymath}r_i=i\Delta S=iv_0\Delta T,\eqno (11)\end{displaymath}$

The values t₀(r_i,s) which have been already found make it possible to find all the experimental data of the primal problem $\tau(T_i),~\mbox{\boldmath$\omega$}(T _i),~T_i=T_0+i\Delta T$ .

Without any loss of generality, assuming for the sound signal propagation velocity in the water c₀=1, we will have

$\begin{displaymath}\tau(T_i)=\Vert\mbox{\boldmath $a$}(r_i,t_0(r_i ,s))\Vert+\Vert\mbox{\boldmath $b$}(r_i,s,t_0(r_i,s))\Vert,\end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $\omega$}(T_i)=\frac{\mbox{\boldmath $b$}(r_i... ...))}{\Vert\mbox{\boldmath $b$}(r_i,s,t_0(r_i,s))\Vert},\eqno(12)\end{displaymath}$

We will only have to simulate the sound power decrease process in the course of its passing through the water from the source to the receiver and the reflection from sea-bottom profile.

As discussed above we assumed that the signal power changes depending upon the length of its path L in the water and obeys the following law:

$\begin{displaymath}P(L)= \frac{P_0}2\left(1-\frac L{\sqrt{\epsilon^2+L^2}}\right).\eqno(13)\end{displaymath}$

Consequently, at the moment when the signal reaches the sea bottom it will have power

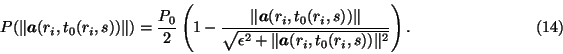
$\begin{displaymath}P( \Vert\mbox{\boldmath $a$}(r_i,t_0(r_i,s))\Vert)=\frac{P_0}... ...mbox{\boldmath $a$}(r_i,t_0(r_i,s)) \Vert^2}}\right).\eqno(14)\end{displaymath}$

We also assume that the signal power decreases at reflection by k₀<1, therefore the power of the signal after the reflection will have the value

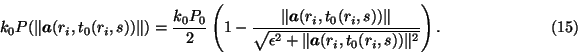
$\begin{displaymath} k_0P(\Vert\mbox{\boldmath $a$}(r_i,t_0(r_i,s))\Vert)=\frac{k... ...mbox{\boldmath $a$}(r_i,t_0(r_i,s))\Vert^2}} \right).\eqno(15)\end{displaymath}$

From these considerations we get the final power of the signal which has reached the receiver

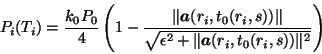
$\begin{displaymath}P_i(T_i)=\frac{k_0P_0}4\left(1-\frac{\Vert\mbox{\boldmath $a$... ...lon^2+\Vert\mbox{\boldmath $a$}(r_i,t_0(r_i,s))\Vert^2}}\right)\end{displaymath}$

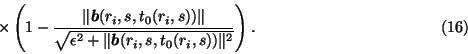
$\begin{displaymath}\qquad\times\left(1-\frac{\Vert\mbox{\boldmath $b$}(r_i,s,t_0... ...mbox{\boldmath $b$}(r_i,s,t_0(r_i,s))\Vert^2}}\right).\eqno(16)\end{displaymath}$

If as a result of the i₀-measurement the power of the signal which has reached the receiver is less than the threshold sensitivity of the transducers, that is, if

$\begin{displaymath}P_{i_0}(T_{i_0})<\delta_0,\eqno(17)\end{displaymath}$

The final solution of the primal problem statement (to be considered) for a collection of experimental data on the passage of a sound signal in the water and its reflection from the sea bottom defined as a curve $\mbox{\boldmath$x$}(t)$ can be formulated as follows.

If in the course of the i-measurement simulation, $i=1,\ldots,n$ , for signal reflected from the sea bottom the inequality $P_i(T_i)>\delta_0$ is fulfilled then the set of experimental data is determined by the relation

$\begin{displaymath} \tau(T_i)=\Vert\mbox{\boldmath $a$}(r_i,t_0(r_i,s))\Vert+\Vert\mbox{\boldmath $b$}(r_i,s,t_0(r_i,s))\Vert, \end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $\omega$}(T_i)=\frac{\mbox{\boldmath $b$}(r_i... ...}{\Vert\mbox{\boldmath $b$}(r_i,s,t_0(r_ i,s))\Vert},\eqno(18)\end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $a$}(r,t)=\mbox{\boldmath $I$}(r)-\mbox{\boldmath $x$}(t),\end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $b$}(r,s,t)=\mbox{\boldmath $P$}(r,s)-\mbox{\boldmath $x$}(t),\eqno(19)\end{displaymath}$

$\begin{displaymath}\langle\mbox{\boldmath $biss$}(r_i,s,t_0),{\mbox{\boldmath $l$}}\,'(t_0)\rangle=0,\eqno(20)\end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $biss$}(r,s,t)=\frac{\mbox{\boldmath $a$}(r,t... ...h $b$}(r,s,t)}{\Vert\mbox{\boldmath $b$}(r,s,t)\Vert}.\eqno(21)\end{displaymath}$

In the opposite case, i.e. if $P_i(T_i)<\delta_0$ , a lot of experimental data is of no importance.

Thus, the basic part of the primal problem solution for collection of experimental data will consist in the search for the roots $t_0(r_i,s)\in(0,b )$ of the equation which has been already obtained

$\begin{displaymath}\langle\mbox{\boldmath $biss$}(r_i,s,t_ 0),{\mbox{\boldmath $l$}}\,'(t_0)\rangle=0.\eqno(22)\end{displaymath}$

Let us make one remark. Depending on the form of the function f(t) which describes the sea-bottom profile and the values of r_i and s, Eq. (24) can possess no solutions at all in the interval (0,b) or it can possess more than one solution (and even infinitely many such solutions).

Let us consider the case when the sea-bottom profile is a lower part of a circle of the radius R with a central point with the radius-vector (R,0),

$\begin{displaymath}f(t)=-\sqrt{R^2-(t-R)^2},\qquad t\in[0,2R],\eqno(23)\end{displaymath}$

Therefore this problem can possess a solution in the case if the radiation source and the radiation receiver are placed symmetrically with respect to the sea-bottom profile circle central point, that is, if R-r_i=s/2. Only in the case when the radiation source and the radiation receiver are in such location we can record the signal reflected from the sea bottom. In all other situations the receiver will not record the reflected signal, that is, as a result of the whole series from n observations we will get data only in the case when R-r_i₀=s/2, and we will obtain $\tau(T_{i_0}),\mbox{\boldmath$\omega$}(T_{i_ 0}).$

However, if during n observations the signal source and the signal receiver are always not in the position which is symmetrical with respect to the sea-bottom profile circle central point then we will not be able to record the reflected signal, and a set of data will be ``empty''. It can lead to an error in the experiment interpretation when this situation will be explained by us due to the fact that the sea-bottom depth is so much large that the reflected signal simply will not be able to reach the receiver.

This example shows that the suggested method of experimental data collection and mathematical approach are not universal and they can in practice lead to wrong conclusions that there is no solution for the sea-bottom profile located at a final depth. This situation is a relatively typical one for inverse problems and reflects the fact that the entire experimental information was collected not completely with respect to the characteristics to be determined.

In the course of conducting the real experiment the situation will not be so hard. The radiation receiver has a small but finite area and the reflected signal is recorded with finite angular resolution. Therefore, signals reflected from the sea bottom will be able to reach the transducer also in the case when the source and the receiver are close to the symmetrical situation, although they will not be exactly symmetrical with respect to the sea-bottom profile circle central point. It will ensure a significant set of data even in this critical case. These counter-examples show limitations of mathematical models to be used and give an indication of their applicability.

Let us give an example of a situation when collecting all the experimental data on the signal reflected from the sea-bottom profile is possible after conducting one observation only.

In the case when the sea-bottom profile is the lower part of the ellipse with focal points located on the axis 0x₁

$\begin{displaymath}f(t)=-\alpha\sqrt{R^2-(t-R)^2},\quad t\in[0,2R],\quad0<\alpha<1\eqno(24)\end{displaymath}$

$\begin{displaymath}r_{i_0}=R(1-\sqrt{1-\alpha^2}),\quad s=2R \sqrt{1-\alpha^2},\eqno(25)\end{displaymath}$

If in such a case as a result of the experiment the signal source and the signal receiver are in described above location, then

$\begin{displaymath}\tau(T_{i_0})=\tau_0, \quad\mbox{if}\quad r_{i_0}=i_0\Delta S=i_0v_0\Delta T.\eqno(26)\end{displaymath}$

All the collected data will make it possible to find the radius-vectors of all profile circle points only according to the results of one such measurement.

This example shows that in a number of cases for the solving of the sea-bottom profile interpolation problem there is no need to conduct a number of n-measurements according to the proposed diagram; conducting only one of them will be sufficient as all the other ones will provide no additional information. It is a common practice to name such problem statements as redeterminated ones. It is further the case which is typical of the inverse problems.

We will name an echo ranging inverse problem the sea-bottom profile interpolation problem on the basis of data on the signal passage time in the water. As opposed to the primal problem one has to deal only with the data obtained as a result of measurements.

Thus, let us assume that we have a set of experimental data $\tau(T_i),\mbox{\boldmath$\omega$}(T_i), i=1,\ldots,n,$ obtained assuming the sound signal passage process in the water; these assumptions have been made earlier. In this case we do not know the sea-bottom profile from which the signal was reflected. To put it otherwise, we do not know the radius-vector $\mbox{\boldmath$x$}(t)$ which must be determined.

$\begin{displaymath}\tau(T_i)=\Vert \mbox{\boldmath $a$}(r_i,t_0(r_i,s))\Vert+\Vert\mbox{\boldmath $b$}(r_i,s,t_0(r_i,s))\Vert,\end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $\omega$}(T_i)=\frac{\mbox{\boldmath $b$}(r_i... ...{\Vert\mbox{\boldmath $b$}(r_i,s,t_0(r_i,s))\Vert} ,\eqno (27)\end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $I$}(r_i)=\mbox{\boldmath $a$}(r_i,t_0(r_i ,s))+\mbox{\boldmath $x$}(t_0(r_i,s)),\end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $P$}(r_i,s)=\mbox{\boldmath $b$}(r_i,s,t_0(r_i,s))+\mbox{\boldmath $x$}(t_0 (r_i,s)).\eqno(28)\end{displaymath}$

The vectors $\mbox{\boldmath$I$}(r_i),~\mbox{\boldmath$P$}(r_i,s)$ can be considered as the ones given as they are fully determined by the known radiation receiver positions aboard the ship and by the preset distance s from the source to the receiver at the instant of conducing any of n measurements. If according to available information: $r_i,s,\tau(T_i),\mbox{\boldmath$\omega$}(T_i),\linebreak i=1,\ldots,n,$ we are able to find any of the vectors $\mbox{\boldmath$a$}(r_i,t_0(r_i,s)),~\mbox{\boldmath$b$}(r_i,s,t_0(r_i,s ))$ , then we will be able to determine also the radius-vector of the point lying on the sea-bottom profile curve from the following relations:

$\begin{displaymath}\mbox{\boldmath $x$}(t_ 0(r_i,s))=\mbox{\boldmath $I$}(r_i)-\mbox{\boldmath $a$}(r_i,t_0(r_i,s)),\end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $x$}(t_0(r_i,s))=\mbox{\boldmath $P$}(r_ i,s)-\mbox{\boldmath $b$}(r_i,s,t_0(r_i,s)).\eqno(29)\end{displaymath}$

Having a set of such points $\mbox{\boldmath$x$}(t_0(r_i,s))$ found as a result of $i=1, \ldots,n$ measurements and connecting them by straight line segments we will be able to find the desired sea-bottom profile interpolation in the form of an open polygon with vectors at these points.

The simplest way is to find the vector $\mbox{\boldmath$b$}(r_i,s,t_0(r_i,s))$ in such a situation, since we have already

$\begin{displaymath}\mbox{\boldmath $b$}(r_i,s,t_0(r_i,s))=\Vert\mbox{\boldmath $... ...r_i,s,t_ 0(r_i,s))\Vert\mbox{\boldmath $\omega$}(T_i)\eqno(30)\end{displaymath}$

It is easy to do it according to the available data $\tau(T_i)$ . And that is the case if

$\begin{displaymath}\mbox{\boldmath $I$}(r_i)=\mbox{\boldmath $a$}(r_i,t_0(r_i,s))+\mbox{\boldmath $x$}(t_0(r_i,s)),\end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $P$} (r_i,s)=\mbox{\boldmath $b$}(r_i,s,t_0(r_i,s))+\mbox{\boldmath $x$}(t_0(r_i,s)),\eqno(31)\end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $P$}(r_i ,s)-\mbox{\boldmath $I$}(r_i)=\mbox... ..._i,s,t_0(r_i,s))-\mbox{\boldmath $a$}(r_i,t_0(r_i,s)).\eqno(32)\end{displaymath}$

With the aim of reducing symbols we will write the arguments hereafter upon which these vectors depend. For example, in the place of the previous equality we can write simply

$\begin{displaymath}\mbox{\boldmath $P$}-\mbox{\boldmath $I$}=\mbox{\boldmath $b$}-\mbox{\boldmath $a$}.\eqno(33)\end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $a$}=\mbox{\boldmath $b$}+(\mbox{\boldmath $I$}-\mbox{\boldmath $P$}).\eqno(34)\end{displaymath}$

Calculating the norm of vectors standing in the last equality and taking into account that

$\begin{displaymath}\Vert\mbox{\boldmath $a$}\Vert=\tau(T_i)-\Vert\mbox{\boldmath $b$}\Vert,\eqno(35) \end{displaymath}$

$\begin{displaymath}\Vert\mbox{\boldmath $a$}\Vert=\tau(T_i)-\Vert\mbox{\boldmath... ...$}+(\mbox{\boldmath $I$}-\mbox{\boldmath $P$}) \Vert.\eqno(36)\end{displaymath}$

If now we take into account that $\mbox{\boldmath$b$}=\Vert\mbox{\boldmath$b$}\Vert\mbox{\boldmath$\omega$}(T_i)$ we can write

$\begin{displaymath}\tau(T_i)-\Vert\mbox{\boldmath $b$}\Vert=\big\Vert\Vert\mbox{... ...+(\mbox{\boldmath $I$}-\mbox{\boldmath $P$})\big\Vert.\eqno(37)\end{displaymath}$

Taking the square of the last equality and using the relation between the norm and the scalar product we will have

$\begin{displaymath}[\tau(T_i)-\Vert\mbox{\boldmath $b$}\Vert]^2= \langle\Vert\m... ...i)+(\mbox{\boldmath $I$}-\mbox{\boldmath $P$})\rangle.\eqno(38)\end{displaymath}$

$\begin{displaymath}[\tau(T_i)-\Vert\mbox{\boldmath $b$}\Vert]^2= \langle\Vert\m... ...t\mbox{\boldmath $b$}\Vert\mbox{\boldmath $\omega$}(T_i)\rangle\end{displaymath}$

$\begin{displaymath}\qquad+\langle \mbox{\boldmath $I$}-\mbox{\boldmath $P$},\mbox{\boldmath $I$}-\mbox{\boldmath $P$}\rangle,\eqno(39)\end{displaymath}$

$\begin{displaymath}\tau^2(T_i)-2 \tau(T_i)\Vert\mbox{\boldmath $b$}\Vert+\Vert\... ...$I$}-\mbox{\boldmath $P$},\mbox{\boldmath $\omega$}(T_i)\rangle\end{displaymath}$

$\begin{displaymath} \qquad+\Vert\mbox{\boldmath $I$}-\mbox{\boldmath $P$}\Vert^2.\eqno(40)\end{displaymath}$

Taking into consideration the fact that $\Vert\mbox{\boldmath$\omega$}(T_i)\Vert=1$ we can find an obvious expression for $\Vert\mbox{\boldmath$b$}\Vert$

$\begin{displaymath}\Vert\mbox{\boldmath $b$}\Vert=[\tau^2(T_i )-\Vert\mbox{\bol... ...dmath $P$},\mbox{\boldmath $\omega$}(T_i) \rangle)\}.\eqno(41)\end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $I$}-\mbox{\boldmath $P$}=-s\mbox{\boldmath $... ... \Vert\mbox{\boldmath $I$}-\mbox{\boldmath $P$}\Vert=s\eqno(42)\end{displaymath}$

$\begin{displaymath}\mbox{\boldmath $\omega$}(T_i)=(\cos\Omega ( T_i),\sin\Omega... ...{\boldmath $\omega$}(T_i)\rangle=-s\cos \Omega (T_i).\eqno(43)\end{displaymath}$

$\begin{displaymath}\Vert\mbox{\boldmath $b$}(r_i,s,t_0(r_i,s))\Vert=[\tau^2(T_i)-s^2]/ \{2[\tau(T_i)-s\cos\Omega (T_i)]\}.\eqno(44)\end{displaymath}$

We have obtained the expression of the radius-vector of the point lying on the sea-bottom profile curve $\mbox{\boldmath$x$}(t_0(r_i,s))$ according to experimental data $\tau(T_i),~\mbox{\boldmath$\omega$}(T_i)$ in the following form:

$\begin{displaymath}\mbox{\boldmath $x$}(t_0(r_i,s))= \mbox{\boldmath $P$}(r_i,s... ...}\mbox{\boldmath $\omega$} (T_i),\qquad i=1,\ldots,n.\eqno(45)\end{displaymath}$

In this section we show the result of computation for the sea-bottom profile interpolation that has been done with the help of ``Maple-V, profile Release 3 for Windows''. Profiles are setting as an analytical form of curves on a plane. Two examples will be given: the first of a rather poor quality of the interpolation because of the unfavourable shape of the sea bottom and the second of a quite good quality. All of obtained diagrams will be represented in the figures. The result of interpolation is compared with a preset sea-bottom profile curve.

$\begin{displaymath}F(x)=-x^{1/25}\exp(0.1x),\end{displaymath}$

$\includegraphics[width=8cm]{kuz9}$

$\textstyle \parbox{0.9\textwidth}{{\small Fig.~9.}~Determination of a sea-botto... ...hick line) described by the formula $F(x)=-0.9[25-(x-5)^2]^{1/2}$(thin line).}$

$\includegraphics[width=8cm]{kuz10}$

$\textstyle \parbox{0.9\textwidth}{{\small Fig.~10.}~Determination of a sea-bott... ...thick line) described by the formula $F(x)=-x^{1/25}\exp(0.1x)$\ (thin line).}$

This work has been carried out in Secondary General Education Technical Lyceum attached to Samara State Technical University under supervision of Dr. Victor P. Tsvetov.