This paper was awarded in the IV International Competition (1995/96) "First Step to Nobel Prize in Physics" and published in the competition proceedings (Acta Phys. Pol. A 92 Supplement, S-21 (1997)). The paper is reproduced here due to kind agreement of the Editorial Board of "Acta Physica Polonica A".
Simulation of Charged Particle Motion in Jupiter's Magnetosphere
M.S. MAHJOURI
Alholton High School, 6520 Freetown Road, Columbia,
MD 21044, USA
Abstract
|
Particle motion in the Jovian magnetodisc is simulated in
a rigidly corotating frame at radial distances from 50 to 150 Jovian radii.
Results are compared with existing Pioneer and Voyager data to determine the
accuracy of the simulation model. Particle orbits are classified into three
distinct classes based on disjoint formations in phase space, and certain
orbits are shown to have chaotic properties. The simulation is used to
determine specific energies required to escape the magnetosphere through the
neutral plane centered at the magnetic equator. The model should help to
explain the detailed features observed for different charged particle species
and energies within the Jovian magnetosphere, and will also provide a
predictive and analytical tool for dealing with Galileo
observations.
PACS numbers: 94.30.Hn, 52.20.Dq
|
1. Introduction
Energetic charged particles play an important role in Jupiter's
magnetosphere. The Pioneer 10/11 and the Voyager 1/2 missions, during their
separate encounters with Jupiter, made measurements that allow for a
derivation of the magnetic field surrounding the planet. Analysis of the data
has revealed that within the magnetosphere there exists an equatorially
elongated magnetic field that is stronger than the general dipole (c.f.
Figs. 1.0, 1.1). This elongation can be modeled by considering the presence
of a thin disc of current flowing in the direction of the azimuth, or
magnetodisc, that extends radially from the planet along the magnetic
equatorial plane to at least 150 planetary radii (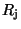 ).
).
It is well known that charged particles follow spiral orbits along dipole
field lines, tending to bounce back and forth between the two planetary
poles. In Jupiter's magnetic field, such particles may become temporarily
trapped in the magnetodisc, bouncing back and forth within the magnetodisc
until they escape to continue the gyrating in the dipolar region outside of
the disc. At low magnetic latitudes (i.e. close to the magnetic equatorial
plane), the magnetodisc causes great curvature in magnetic field lines. Few
particles can negotiate these sharp magnetic turns and maintain the magnetic
moment, which is proportional to the magnetic flux enclosed by the particle's
spiral radius (gyroradius). Since the magnitude of magnetic force varies
roughly as the inverse cube of radial distance from Jupiter, the gyroradii of
energetic ions will increase accordingly. In some cases, the gyroradii of
such ions may exceed the curvature radius of magnetic field lines within the
magnetodisc and cause the ions to undergo nonadiabatic motion. This highly
nonlinear motion, unpredictable within the magnetodisc, falls within the
realm of deterministic chaos. Particles that travel through such orbits are
discussed in Sec. 4. Once trapped inside the magnetodisc, a particle's motion
can be broken down into two components: a ``bouncing'' motion perpendicular
to the magnetodisc, and a semicircular motion on the magnetodisc plane. The
semicircular motion in the magnetodisc plane can cause the particle to drift
radially outward, to the extent that it travels outside the effective realm
of the magnetosphere. It is shown in Sec. 6 that the probability for such
ions to escape is highly dependent on initial injection energy.
All physical predictions are based on a computer code that will model
particle motion in Jupiter's magnetosphere. This motion is determined by
integrating the Lorentz force using the best existing model for the Jovian
magnetosphere. At a given energy, the code simulates injection with an
isotropic pitch angle distribution, and allows for isolation of different
particles and different points of injection.
The available data reveal that the velocity distributions of ions are not
isotropic in phase-space, a factor that is most likely due to the stretching
effect of the magnetodisc on the magnetic field. The validity of the computer
experiment described herein is verified by garnering distributions that agree
with the observed data. Section 5 shows that the distributions obtained
through this simulation are consistent with those detected by the Pioneer
spacecraft.
The Galileo spacecraft, which will begin orbiting Jupiter in December 1995,
carries several instruments that will measure characteristics of Jupiter's
magnetosphere, including its magnetic field, plasma, and energetic charged
particle populations. The Energetic Particle Detector (EPD) will provide
information regarding the activity of high energy ions and electrons within
the Jovian magnetosphere. This simulation will be used as a tool to predict
and explain observations made by the spacecraft.
Because Jupiter's magnetic axis is at an angle to its rotation axis, the
magnetodisc tends to flap up and down causing periodic fluctuations in data.
Since this behavior is similar to that expected to exist in pulsars, a
detailed study of Jupiter's magnetodisc may also provide insight into issues
of astrophysical interest.
2. Preliminaries
2.1. General definitions associated with charged particles in a magnetic field
The time rate of change of momentum for a particle with charge q and mass
m in a magnetic field B and electric field E is described by the
experimentally determined Lorentz force, which is (in the units of Gaussian
CGS)
where x is the particle's position vector
from a given reference point, v is the particle's velocity, and c is
the speed of light (approximately
3 x 1010 cm/s). According to
special relativity, the momentum p is given by
where the Lorentz factor is
To clarify the nature of the
force in Eq. (1), we derive an expression for the time rate of change of
kinetic energy W by taking the dot product of the velocity with both sides
of Eq. (1) to show that
Equation (4) shows that, in the absence of an electric field
(i.e.
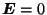 ), kinetic energy is constant. Put simply, a magnetic field
cannot change the kinetic energy of a particle. Equation (1) can be solved
analytically to show that particles in a static uniform magnetic field, i.e.
), kinetic energy is constant. Put simply, a magnetic field
cannot change the kinetic energy of a particle. Equation (1) can be solved
analytically to show that particles in a static uniform magnetic field, i.e.
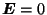 and B = constant, spiral (gyrate) along field lines. The
previous description can be applied to a particle's instantaneous position in
the magnetosphere when the magnetic field varies with position but can be
assumed to be constant with time. Such particles have an instantaneous
orbital frequency (gyrofrequency) of
and B = constant, spiral (gyrate) along field lines. The
previous description can be applied to a particle's instantaneous position in
the magnetosphere when the magnetic field varies with position but can be
assumed to be constant with time. Such particles have an instantaneous
orbital frequency (gyrofrequency) of
and orbital radius (gyroradius)
where 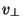 is the component of velocity that is perpendicular to the local magnetic
field B. Equation (5) allows us to define the period of one gyration
as
is the component of velocity that is perpendicular to the local magnetic
field B. Equation (5) allows us to define the period of one gyration
as
We also define a pitch
angle 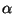 , which is the angle between the velocity vector v and the
magnetic field B at any point x, such that
, which is the angle between the velocity vector v and the
magnetic field B at any point x, such that
where 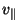 is the component of the
particle's velocity parallel to the direction of the local magnetic field.
is the component of the
particle's velocity parallel to the direction of the local magnetic field.
2.2. Adiabatic invariants
Equations (1-8) allow us to draw an important conclusion regarding the
predictability of particle motion in a known magnetic field. If the magnetic
field varies slowly over space, i.e.
and slowly over time, i.e.
then the ratio of perpendicular component of kinetic
energy, 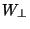 , to the magnitude of the magnetic field, B, is
approximately invariant. This is called the first adiabatic invariant, or
magnetic moment, and is expressed as follows:
, to the magnitude of the magnetic field, B, is
approximately invariant. This is called the first adiabatic invariant, or
magnetic moment, and is expressed as follows:
For Jupiter,
conditions (9) and (10) are true at high magnetic latitudes where the
magnetic field is well approximated by that of a magnetic dipole, and the
first adiabatic invariant (11) is a constant of the motion.
Consider a system in which there is no electric field E parallel to the
time-independent magnetic field. Then a particle's kinetic energy remains
constant, and can be expressed as
In a field where the first adiabatic invariant is conserved, Eq. (11) shows
that, as the magnetic field strength increases (e.g. as a particle following
a dipole field line gets closer to a pole), the pitch angle must also
increase. At a given ``mirror point'' (where the pitch angle increases to 90
degrees) 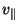 decreases, goes through zero and changes signs. For
certain B fields that satisfy (9) and (10), e.g., those of dipolar forms,
a charged particle oscillates periodically between two such mirror points,
and it is possible to define a second conserved quantity
decreases, goes through zero and changes signs. For
certain B fields that satisfy (9) and (10), e.g., those of dipolar forms,
a charged particle oscillates periodically between two such mirror points,
and it is possible to define a second conserved quantity
where 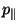 denotes momentum parallel to the magnetic
field, s describes distance traveled along the field line, m1 and m2
are mirror points, and Bm is the magnitude of the magnetic field at either
mirror point. Equation (13) defines the second adiabatic invariant of motion,
and is constant in a field satisfying (9) and (10).
denotes momentum parallel to the magnetic
field, s describes distance traveled along the field line, m1 and m2
are mirror points, and Bm is the magnitude of the magnetic field at either
mirror point. Equation (13) defines the second adiabatic invariant of motion,
and is constant in a field satisfying (9) and (10).
The motion of a particle gyrating in a field in which the first and second
adiabatic invariants are conserved is easily predictable if the magnetic
field strength is known. Such motion can be expected for charged particles in
the dipolar region (well above or below the magnetodisc) of the Jovian field.
However, as particles move into the current disc, the radial component of the
magnetic field changes direction, and conditions (9) and (10) are not
satisfied. In this region, particles undergo nonadiabatic motion; the highly
nonlinear dynamics of nonadiabatic motion can produce observed anisotropies
in the measured densities of high energy protons [1].
2.3. Guiding center theory
When conditions (9) and (10) are satisfied, a charged particle's motion
consists of a velocity component along B plus a slow drift velocity
perpendicular to B. Using (1) and averaging particle motion over a
gyroperiod yields the following expression for momentum [2]:
where
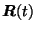 represents the particle's guiding center at time t. Taking
the cross product of B with both sides of (14), assuming time independent
B and E fields, and considering the case that the particle's parallel
velocity is much greater than its perpendicular guiding center velocity, it
is possible to express the component of the particle's guiding center
velocity perpendicular to the magnetic field as follows:
represents the particle's guiding center at time t. Taking
the cross product of B with both sides of (14), assuming time independent
B and E fields, and considering the case that the particle's parallel
velocity is much greater than its perpendicular guiding center velocity, it
is possible to express the component of the particle's guiding center
velocity perpendicular to the magnetic field as follows:
The three terms on the
right hand side of Eq. (15) represent the ``
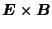 drift,''
``grad-B drift,'' and ``curvature drift'', respectively. In all terms,
both B and E are evaluated at the guiding center R. In a
planetary dipole with a cylindrical coordinate system centered on the planet,
the effects of the drifts for higher energy particles in Eq. (15) would be
most pronounced in the azimuthal (
drift,''
``grad-B drift,'' and ``curvature drift'', respectively. In all terms,
both B and E are evaluated at the guiding center R. In a
planetary dipole with a cylindrical coordinate system centered on the planet,
the effects of the drifts for higher energy particles in Eq. (15) would be
most pronounced in the azimuthal (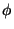 ) component. As will be shown in
Sec. 6, the effects of the guiding center drifts can couple with rapid
oscillations induced by the current disc for higher energy particles, setting
a particle's orbit on a hyperbolic drift trajectory and allowing it to
effectively escape the magnetosphere from inside the magnetodisc.
) component. As will be shown in
Sec. 6, the effects of the guiding center drifts can couple with rapid
oscillations induced by the current disc for higher energy particles, setting
a particle's orbit on a hyperbolic drift trajectory and allowing it to
effectively escape the magnetosphere from inside the magnetodisc.
2.4. Jupiter's magnetic field
Magnetometers carried by the Pioneer 10/11 and Voyager 1/2 spacecraft
measured Jupiter's magnetic field. In addition, charged particle detectors on
Pioneer 10 recorded ten hour flux rates of energetic charged particles. This
periodic fluctuation of measurements is caused by the existence of a current
sheet aligned with the magnetic pole and at an angle to the rotational pole.
Randall [3] and Van Allen et al. [4] have used the fact that charged
particles tend to follow magnetic field lines to deduce a 10 degree tilt
angle between the planet's rotational and dipole axes. Northrop et al. [5]
interpreted delays in expected particle fluxes as due to the finite. Alfven
wave propagation, i.e., the delay between planetary rotation and subsequent
rotation of the outer parts of the distant magnetosphere, such that field
lines deviate from the meridian plane and have an azimuthal component. Smith
et al. [6] interpret 10 hour particle fluxes as due to the existence of an
extended current sheet along the magnetic equator. Goertz et al. [7] use the
Pioneer 10 magnetometer and charged particle observations to produce a
mathematical model for the Jovian magnetic field. The magnetic field consists
of the superposition of a dipole field with that produced by a current disc
in the plane of the magnetic equator. In cylindrical coordinates, the two
fields are given by
dipole:



current sheet:
where
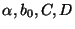 are constants determined by
fitting the Pioneer 10 data (Table (1.0)),
are constants determined by
fitting the Pioneer 10 data (Table (1.0)), 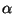 is the exponent of
magnetodisc radial variation, b0 is the disc field variable, C is the
dimensionless constant, D is the disc thickness. In Eqs. (16), the constant
M is the Jovian dipole moment, found in Table (1.1).
is the exponent of
magnetodisc radial variation, b0 is the disc field variable, C is the
dimensionless constant, D is the disc thickness. In Eqs. (16), the constant
M is the Jovian dipole moment, found in Table (1.1).
| Table 1.0. Magnetic field constants fit to Pioneer 10 magnetometer data. |
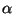 |
b0 |
C |
D |
| 0.7 |
9 x 10-2
G |
10 |
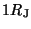 |
| Table 1.1. Pertinent physical values for Jupiter. |
| Planetary radius |
Dipole moment |
Planetary rotation period |
Orbital frequency |
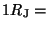 7.1492 x 109 cm
7.1492 x 109 cm |
4.2 Gauss
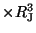 |
10 h |
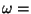 1.745 x 10-4 rad/s
1.745 x 10-4 rad/s |
Although the Voyager data is more recent, Voyager models of the magnetic
field are reliable only out to 30 Jovian radii, and the goal is to simulate
particle motion in the range of 50-150 Jovian radii. Therefore, the field
provided by Goertz et al. [7] with Pioneer 10 data is used. The magnetic
field model can then be expressed as
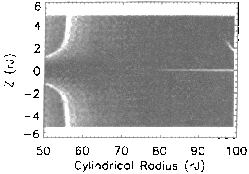
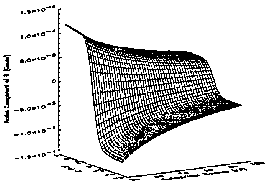
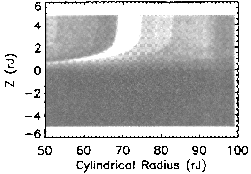
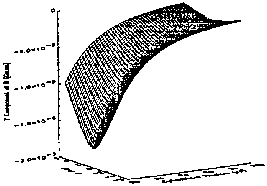
Figures 1.0-1.5 display the field strength and
components as labeled, and clearly illustrate the local minimum, or magnetic
``well'' in the field magnitude created by the current disc near the magnetic
equatorial plane. Figure 1.6 shows that the radius of curvature for any field
line is minimum on the magnetic equatorial plane, and that this curvature
radius decreases as radial distance from the planet increases. The ``sharp
turns'' of field lines about the magnetic equator, i.e., inside the current
disc, cause the direction of the magnetic field to change abruptly. This
rapid spatial variation of the magnetic field inside the magnetodisc does not
satisfy Eq. (9), which requires a slow variation over space. Therefore,
nonadiabatic and highly nonlinear motion near the current disc is to be
expected.
 |
|
 |
| Fig. 1.0. Field strength. |
|
Fig. 1.1. Field strength. |
| |
|
|
 |
|
 |
| Fig. 1.2. Radial field. |
|
Fig. 1.3. Radial field. |
| |
|
|
 |
|
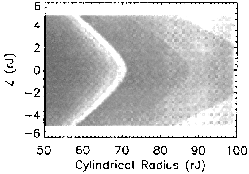 |
| Fig. 1.4. Z field. |
|
Fig. 1.5. Z field. |
| |
|
|
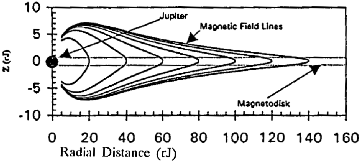 |
| Fig. 1.6. Jovian field lines. |
3. Basic method
Using the magnetic field model provided by Goertz et al. [7], we simulate
charged particle motion through Jupiter's magnetosphere and into the
magnetodisc. Particles are injected isotropically in velocity space. We
perform different runs of the program by injecting electrons and various ion
species, and systematically varying the particle energy to analyze motion
within the magnetodisc.
To simplify calculations, we choose a reference frame that is corotating
rigidly with the magnetospheric plasma that is trapped on magnetic field
lines. In this corotating frame the electric field due to rotating plasma
vanishes. We account for the coriolis and centrifugal forces that arise in
this noninertial reference frame, and transform (1), using the subscript r to
denote that a function is evaluated in the rotating (noninertial) frame
B is given by (18),
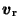 denotes the
particle's velocity in the corotating frame,
denotes the
particle's velocity in the corotating frame, 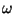 is the angular velocity
of the corotation frame about the rotation axis, and
is the angular velocity
of the corotation frame about the rotation axis, and 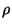 is the particle's
cylindrical radius as measured from the planet. To corotate with Jupiter's
magnetosphere, we set
is the particle's
cylindrical radius as measured from the planet. To corotate with Jupiter's
magnetosphere, we set 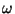 equal to the rotational frequency of the
planet, as given in Table (1.1). The centrifugal and coriolis forces, present
in any rotating reference frame, are represented by the second and third
terms of (19), respectively. Taking the scalar product of the rotational
velocity with both sides of (19) yields a quantity that must be conserved
during particle motion. This conserved quantity is the sum of the particle's
kinetic energy and its centrifugal potential energy
equal to the rotational frequency of the
planet, as given in Table (1.1). The centrifugal and coriolis forces, present
in any rotating reference frame, are represented by the second and third
terms of (19), respectively. Taking the scalar product of the rotational
velocity with both sides of (19) yields a quantity that must be conserved
during particle motion. This conserved quantity is the sum of the particle's
kinetic energy and its centrifugal potential energy
For calculating particle densities (i.e. simulating several thousand particle
orbits), Eqs. (16) and (17) can be costly in terms of computer time.
Calculations are simplified by evaluating the magnetic field on a two
dimensional grid, and using a combination of table lookup and bilinear
interpolation found in Ref. [8].
Integration of (19) for the three components of position and corresponding
velocity is accomplished using a fifth-order Runge-Kutta numerical
integration procedure. An adaptive stepping algorithm found in Ref. [9] and
coded in Numerical Recipes in C (Vers 2.0) is slightly modified
and used to speed the integration process. A random number generator, also
found in Numerical Recipes in C (Vers. 2.0) is used to generate
random initial conditions. Numerical accuracy is monitored by assuring that
the orbital invariant (22) remains constant to within 1 part in 103.
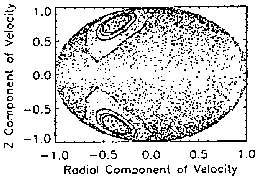
4. Single orbits
Particle orbits in the Jovian field can be classified roughly into three
categories: bounded, transient, and stochastic. Figures 2.0-2.1
show a transient orbit that characteristically follows the expected dipolar
orbit until it hits the current disc. Once inside, it bounces around
unpredictably, but quickly exits the magnetodisc to continue gyrating in a
predictable fashion. The time spent within the magnetodisc is very small, and
once ``outside'' the particle continues gyrating in the dipolar region of the
field until it ``mirrors'' back into the magnetodisc. Another type of orbit,
not shown, is the bounded or ``regular'' orbit, that can only exist for
particles injected in the magnetodisc. Bound orbits are permanently trapped
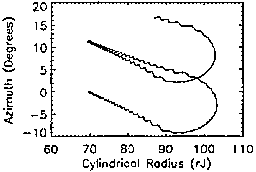
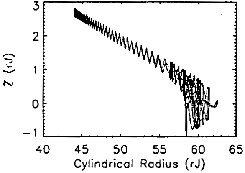
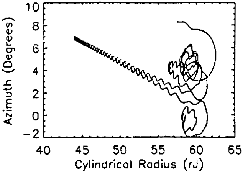
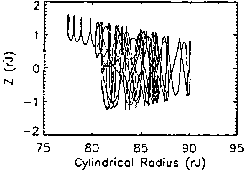
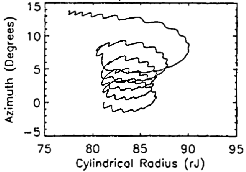
within the magnetodisc. Figures 2.2-2.5 show stochastic orbits. Such orbits
exhibit adiabatic characteristics outside the magnetodisc region, but become
trapped for long periods of time within the current disc. Once within the
current disc, the particle undergoes motion similar to that of a bounded
orbit, but with far less periodicity. Unlike bounded orbits, however,
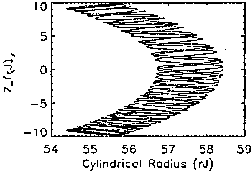
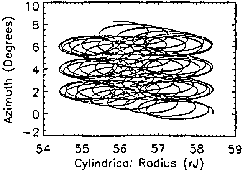
stochastic orbits eventually exit the magnetodisc region. Figures 2.6-2.7
show particle motion in a dipole field, and serve as an example of pure
adiabatic motion.
Stochastic orbits temporarily trapped within the magnetodisc cross the
magnetic equatorial plane many times, while transient orbits tend to cross it
once or twice. The number of equatorial crossings of bounded orbits is
unlimited. Particles are injected at a single point in the ``neutral plane'',
i.e., z=0, and various components of motion at subsequent neutral plane
crossings are recorded. This technique, titled the ``Poincare surface of
section'', allows otherwise undetectable properties of the three different
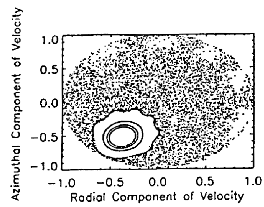
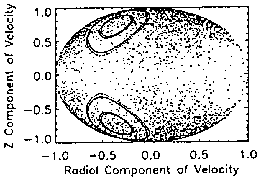
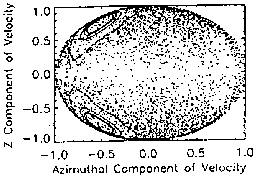
particle orbits to be explored. Figures 3.0-3.7 show particle behavior in a
Poincare surface of section for various injection energies. Normalized
particle velocities are recorded at plane crossings to show that the bound,
transient, and stochastic orbits populate finite boundaries within phase
space. The regions created by bounded orbits consist of the tightly bounded
concentric circular formations, each of which represents the crossings of a
single trapped particle, and whose radius depends upon injection velocity. It
becomes clearly visible that the bound orbits are confined to a particular
``circle'', which implies that their motion is governed by some
invariant [10]. Stochastic orbits populate the region outside the concentric
circles, which is characterized by the large distribution of crossing points.
No unperturbed orbit can cross between the stochastic and bounded regions.
Stochastic orbits present a remarkable characteristic, namely, that the
distance in phase space between two orbits with nearly identical injection
coordinates will diverge exponentially with time. Stochastic orbits from
particles injected at any differential initially stochastic region in the
phase space will entirely cover the stochastic region, regardless of what
region is chosen. The space is shown to be ``sticky'', as stochastic orbits
can come arbitrarily close to the bounded region and become trapped for
indefinitely long time periods, a property shown in Fig. 6, where no bounded
orbits exist (particles are injected outside of the magnetodisc), but the
outline of the bounded region is marked by ``sticky'' stochastic orbits. This
characteristic is most clearly evident in Fig. 2.5, where the circular
bounces of the stochastic orbit in the 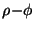 plane mimic bounded
orbit motion. Transient orbits populate the sparse regions characterized by
the seeming ``bald spots'' on the figures. Transient orbits cross the neutral
plane only a few times per magnetodisc entry, so their presence in a space
populated by ``full-time'' bounded orbits and ``part-time'' stochastic orbits
is relatively scarce. Accordingly, Fig. 3 shows only a few points in the
transient region. Transient orbits can, however, move into the stochastic
region from a few particular transient points after occupying a series of
transient regions.
plane mimic bounded
orbit motion. Transient orbits populate the sparse regions characterized by
the seeming ``bald spots'' on the figures. Transient orbits cross the neutral
plane only a few times per magnetodisc entry, so their presence in a space
populated by ``full-time'' bounded orbits and ``part-time'' stochastic orbits
is relatively scarce. Accordingly, Fig. 3 shows only a few points in the
transient region. Transient orbits can, however, move into the stochastic
region from a few particular transient points after occupying a series of
transient regions.
 |
|
 |
| Fig. 2.0 |
|
Fig. 2.1 |
| |
|
|
 |
|
 |
| Fig. 2.2 |
|
Fig. 2.3 |
| |
|
|
 |
|
 |
| Fig. 2.4 |
|
Fig. 2.5 |
| |
|
|
 |
|
 |
| Fig. 2.6 |
|
Fig. 2.7 |
 |
|
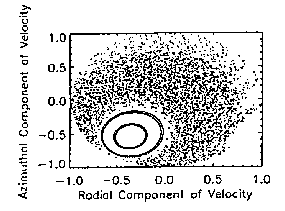 |
| Fig. 3.0. 10 KeV protons. |
|
Fig. 3.1. 100 KeV protons. |
| |
|
|
 |
|
 |
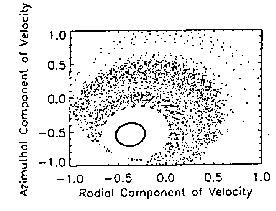
| Fig. 3.2. 1 MeV protons. |
|
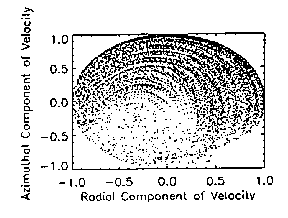
Fig. 3.3. 10 MeV protons. |
| |
|
|
 |
|
 |
| Fig. 3.4. 10 KeV protons. |
|
Fig. 3.5. 100 KeV protons. |
| |
|
|
 |
|
 |
| Fig. 3.6. 1 MeV protons. |
|
Fig. 3.7. 10 MeV protons. |
 |
|
 |
| Fig. 3.8. 10 KeV protons. |
|
Fig. 3.9. 100 KeV protons. |
| |
|
|
 |
|
 |
| Fig. 3.10. 1 MeV protons. |
|
Fig. 3.11. 10 MeV protons. |
| |
|
|
 |
|
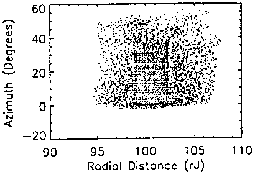 |
| Fig. 3.12. 10 KeV protons. |
|
Fig. 3.13. 100 KeV protons. |
| |
|
|
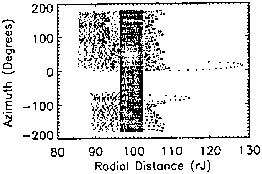 |
|
 |
| Fig. 3.14. 1 MeV protons. |
|
Fig. 3.15. 10 MeV protons. |
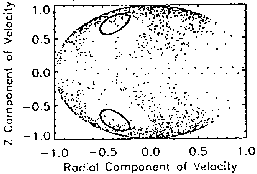
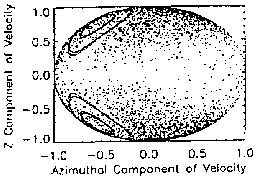
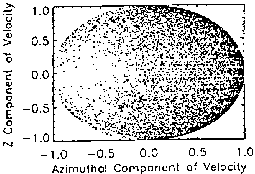
If plotted in three dimensional phase space, the crossing velocities shown in
Fig. 3 would map directly onto a sphere. Figures 3.3-3.7 demonstrate that
such a sphere would be bilaterally symmetrical upon the radial velocity axis.
Such an assertion is rather obvious, since a bounded orbit would require
oppositely changing z velocity at every crossing in order to maintain its
circular orbit on the surface of section. The near symmetry about the
horizontal line bisecting Figs. 3.3-3.7 serves to validate the accuracy of
the simulation model.
The structure of the phase space formation is highly dependent on the z
component of the magnetic field. A particle under the influence of two
perfectly antiparallel field lines would undergo either a figure eight motion
around both field lines, or it would spiral around one field line. To analyze
chaotic motion, a quantity
is defined, and the field line equatorial radius of curvature, 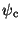 , is calculated to be
, is calculated to be
As 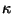 approaches unity, the level of
chaos in the magnetodisc, measured by the percentage of stochastic orbits, is
maximized. For a one dimensional system depending only on z, Buchner and
Zeleny [11] have shown this behavior analytically and Chen and Palmadesso
[10] have proven it numerically. Karimabadi et al. [12] arrive at this result
for a family of two dimensional field models similar to the Jovian field
model in (16-18). The values of
approaches unity, the level of
chaos in the magnetodisc, measured by the percentage of stochastic orbits, is
maximized. For a one dimensional system depending only on z, Buchner and
Zeleny [11] have shown this behavior analytically and Chen and Palmadesso
[10] have proven it numerically. Karimabadi et al. [12] arrive at this result
for a family of two dimensional field models similar to the Jovian field
model in (16-18). The values of 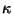 , gyroradius, and curvature radius
based on the field (16-18) are represented in Fig. 4. Buchner and Zeleny
[11] found that for
, gyroradius, and curvature radius
based on the field (16-18) are represented in Fig. 4. Buchner and Zeleny
[11] found that for 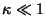 , there is still a significant amount of
chaos within the system. Particle behavior near the current sheet is then not
only nonadiabatic, but also chaotic.
, there is still a significant amount of
chaos within the system. Particle behavior near the current sheet is then not
only nonadiabatic, but also chaotic.
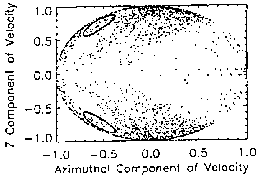
Upon first glance, Fig. 3.3 fails to show the structure evident for particles
of lower energies. The 10 meV particles yield a 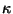 value that is
approximately 17% smaller than that for the 10 keV particles. Accordingly,
the bounded space is replaced by stochastic orbits, which indicates a greater
amount of chaos, as (23) predicts. This effect is evident in the diminution
of bound orbit islands as injection energy increases. However, a
17% decrease in
value that is
approximately 17% smaller than that for the 10 keV particles. Accordingly,
the bounded space is replaced by stochastic orbits, which indicates a greater
amount of chaos, as (23) predicts. This effect is evident in the diminution
of bound orbit islands as injection energy increases. However, a
17% decrease in 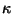 cannot virtually eliminate all bounded orbits, as
is suggested by Fig. 3.3. Each bounded particle seems confined to a
semicircle in the
cannot virtually eliminate all bounded orbits, as
is suggested by Fig. 3.3. Each bounded particle seems confined to a
semicircle in the 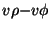 plane. It is entirely possible that the
bounded orbits do exist in their complete circular form, but that they escape
the system radially before they can complete their circular phase space
formation. This is more plausible than the complete elimination of bounded
orbits, and leads to the concept of energy drop-off that is discussed in
Sec. 6. In fact, the ratio of particles that escaped radially to particles
that remained trapped indefinitely in Fig. 3.3 was much greater at 10 meV
than at the lower energies. A slightly greater number of points lie in the
positive radial velocity hemisphere (Fig. 3.7 shows this best) and a large
majority also lie on the positive azimuthal hemisphere (Fig. 3.3).
plane. It is entirely possible that the
bounded orbits do exist in their complete circular form, but that they escape
the system radially before they can complete their circular phase space
formation. This is more plausible than the complete elimination of bounded
orbits, and leads to the concept of energy drop-off that is discussed in
Sec. 6. In fact, the ratio of particles that escaped radially to particles
that remained trapped indefinitely in Fig. 3.3 was much greater at 10 meV
than at the lower energies. A slightly greater number of points lie in the
positive radial velocity hemisphere (Fig. 3.7 shows this best) and a large
majority also lie on the positive azimuthal hemisphere (Fig. 3.3).
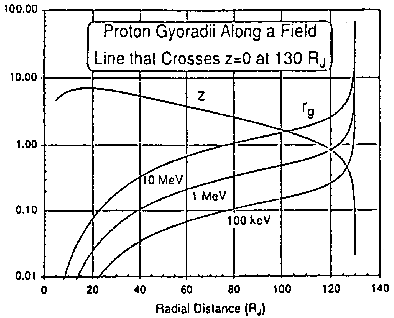
Fig. 4.0
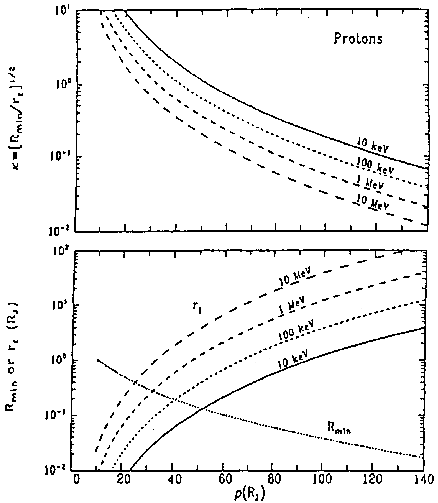
Fig. 4.1
Thus, there is a tendency for 10 meV protons to head in the positive
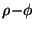 direction, the direction of escape. The radial component of
velocity does appear to be cycling in the relatively expected way, but,
assuming there are no ``double loops'', the particle must always travel in
the positive azimuthal direction to satisfy the surface of section. The
10 meV particles follow a serpentine motion, and their crossings with the
neutral plane trace out a semicircle.
direction, the direction of escape. The radial component of
velocity does appear to be cycling in the relatively expected way, but,
assuming there are no ``double loops'', the particle must always travel in
the positive azimuthal direction to satisfy the surface of section. The
10 meV particles follow a serpentine motion, and their crossings with the
neutral plane trace out a semicircle.
5. Probable regions
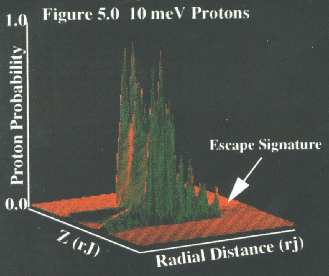
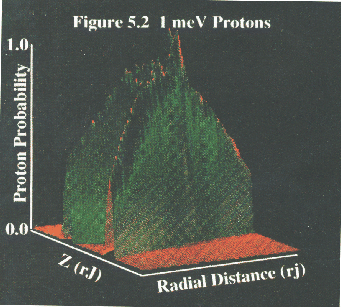
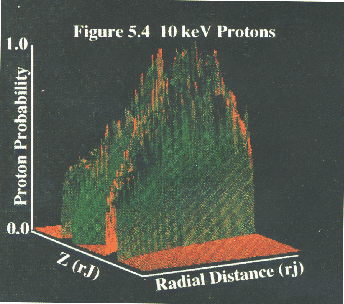
Figure 5 shows distributions of spatial density within 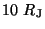 for
protons injected uniformly in the radial range from 50 to
for
protons injected uniformly in the radial range from 50 to 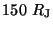 , with
z-component of
, with
z-component of 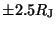 . The pitch angle distribution is isotropic at
injection. The distributions are relatively symmetric about the z-axis as
expected. The curved ``root-like'' appearance of the densities in Fig. 5 is
consistent with the field model in Fig. 1, and can be attributed to the
cutoff of the radial component of initial injection. The density enhancement
evident within
. The pitch angle distribution is isotropic at
injection. The distributions are relatively symmetric about the z-axis as
expected. The curved ``root-like'' appearance of the densities in Fig. 5 is
consistent with the field model in Fig. 1, and can be attributed to the
cutoff of the radial component of initial injection. The density enhancement
evident within
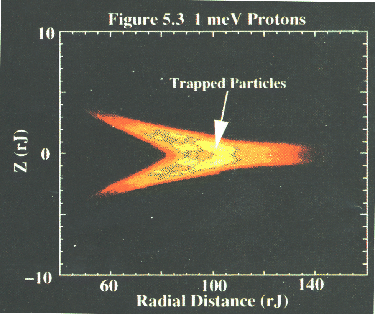
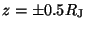 shows that the particles are being
temporarily trapped within the magnetodisc, again, as expected. With the
current disc oscillating as the planet rotates, these trapped particles in
the magnetodisc account for the square-wave modulation of particle count
rates detected by the University of Iowa instrument abroad Pioneer 10 in the
region of 50-
shows that the particles are being
temporarily trapped within the magnetodisc, again, as expected. With the
current disc oscillating as the planet rotates, these trapped particles in
the magnetodisc account for the square-wave modulation of particle count
rates detected by the University of Iowa instrument abroad Pioneer 10 in the
region of 50-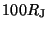 , as shown in Fig. 1 in Ref. [7]. The simulation is
consistent with these data.
, as shown in Fig. 1 in Ref. [7]. The simulation is
consistent with these data.
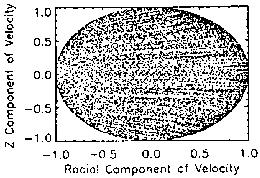
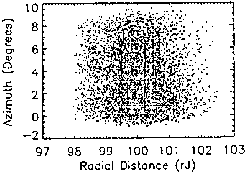
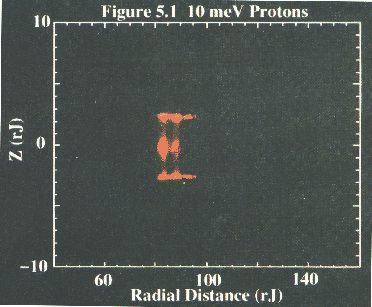
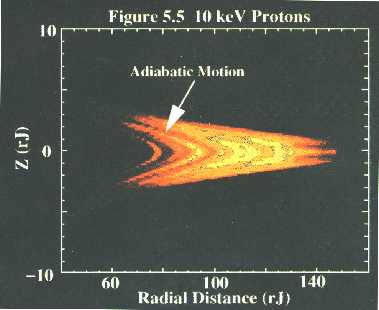
A highly informative feature in the spatial surface of section plots (azimuth
versus radius), most obvious for 10 meV particles, is the subtle appearance
of ``tracks'' extending radially outward, away from the clumped region. As
Figs. 3.15 (10 meV protons) and 6.5-6.6 (10 meV protons) indicate, there is
a current disc ``escape route'' for higher energy particles. Because of their
escape, these make negligible contribution to the density, especially when
compared to stochastic orbits that mimic bounded particles. However, the
escaping particles are dense enough to leave a small track behind.
6. Effect of initial energy and injection 
6.1. Analytic argument
The field given by
is inversely proportional to some power of the
cylindrical distance from the planet. The 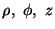 components of the
Newton-Lorentz equations for such a field are as follows:
components of the
Newton-Lorentz equations for such a field are as follows:
 |
|
 |
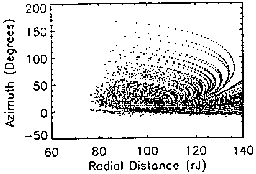
| Fig. 6.0. 52 rj. |
|
Fig. 6.1. 68 rj.. |
| |
|
|
 |
|
 |
| Fig. 6.2. 82 rj. |
|
Fig. 6.3. Positron at 82 rj. |
| |
|
|
 |
|
 |
| Fig. 6.4. 52 rj. |
|
Fig. 6.5. 68 rj. |
| |
|
|
 |
|
 |
| Fig. 6.6. 82 rj. |
|
Fig. 6.7. Positron at 82 rj. |
Multiplying (26b) by 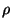 and transforming it into differential
form shows that for
and transforming it into differential
form shows that for 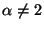 the quantity
the quantity
is conserved. Defining the local gyrofrequency at
injection 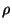 as
as
such that (27) becomes a quadratic of the form
The next step is to find the maximum cylindrical radius given initial 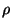 and initial velocity. To simplify matters, it is assumed that the injection
velocity has only a
and initial velocity. To simplify matters, it is assumed that the injection
velocity has only a 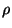 component (
component (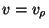 ), i.e., it is perpendicular
to the magnetic field. Then, it is possible to substitute the velocity at any
point divided by the initial gyrofrequency for the initial gyroradius. Then,
(29) transforms into
), i.e., it is perpendicular
to the magnetic field. Then, it is possible to substitute the velocity at any
point divided by the initial gyrofrequency for the initial gyroradius. Then,
(29) transforms into
where
For a particle to escape, the initial conditions
must be such (30) has an imaginary root, i.e., 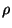 goes to infinity.
According to Pioneer 10 data, the exponent of the Jovian magnetic field comes
out to about 2.7. It is appropriate to estimate (30) for
goes to infinity.
According to Pioneer 10 data, the exponent of the Jovian magnetic field comes
out to about 2.7. It is appropriate to estimate (30) for 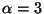 (the
fall off rate for a magnetic dipole), in which case (30) has the physically
significant root
(the
fall off rate for a magnetic dipole), in which case (30) has the physically
significant root
which
reveals that, for the specified simplifications, a particle can theoretically
escape through the z=0 plane if its initial energy satisfies
6.2. Radial dependence
The probability of escaping through the magnetodisc is also dependent on
injection radius. It is prudent to use surface of section plots to illustrate
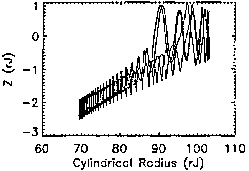
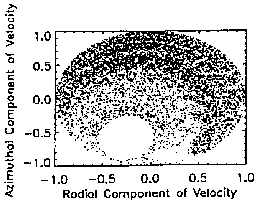
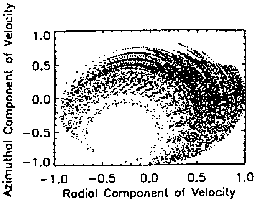
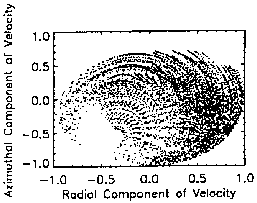
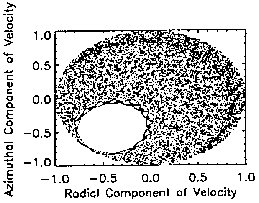
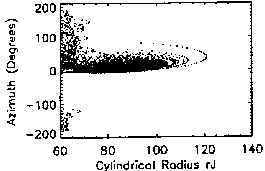
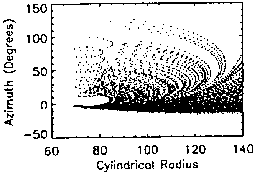
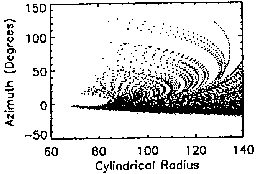
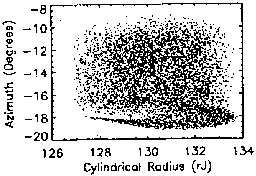
this dependence. In Fig. 6, 10 meV protons are injected at
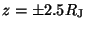 ,
to simulate injection into the current disc from high latitudes. This
eliminates bound orbits, which can only exist if the particle is injected in
the current disc, reemphasizes stochastic orbit properties, and simulates a
more realistic situation. The positron is plotted (Figs. 6.3, 6.7) because
its small mass relative to that of a proton will allow it to map along the
field line out to the radius where the field line crosses the equatorial
plane. It serves as an accuracy ``check'' of the simulation.
,
to simulate injection into the current disc from high latitudes. This
eliminates bound orbits, which can only exist if the particle is injected in
the current disc, reemphasizes stochastic orbit properties, and simulates a
more realistic situation. The positron is plotted (Figs. 6.3, 6.7) because
its small mass relative to that of a proton will allow it to map along the
field line out to the radius where the field line crosses the equatorial
plane. It serves as an accuracy ``check'' of the simulation.
Figures 6.0-6.3 show the evolution of the phase-space coordinates as
radial distance increases. The preponderance of points tending toward the
positive (outward) radial velocity hemisphere indicate a clear tendency
toward escape as injection radial distance increases. The position plots
(Figs. 6.4-6.6) show the particles performing a giant semicircular motion
through subsequent crossings. As injection radius increases, however, fewer
and fewer particles reach the ``reversal-point'' required to complete the
loop and head back inward. As they circle outward, the fields is also getting
weaker, and the curvature radius of their semicircle is increasing. A
fraction of these orbits can become radially unbounded, and not come back
inward, even if a radial ``cutoff'' boundary in not specified.
6.3. Numerically calculated energy drop-offs
The preceding findings suggest the presence of an escape mechanism in the
magnetodisc, by which particles can radially exit the magnetosphere. To prove
this numerically, we set up a simulation in which we inject particles at a
single radius, but still at
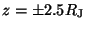 . The four energies of interest
are: 10 meV, 1 meV, 100 keV, and 10 keV. This covers the energy range
relevant to energetic particle detectors on the Pioneer, Voyager, and Galileo
spacecraft. The effect of injection radius, demonstrated qualitatively for
10 meV particles in Fig. 6, is tested quantitatively by limiting injection to
a single radius and varying that radius in subsequent runs. For each
injection radius, four separate simulations are executed, one for each of the
aforementioned energies. The number of particles that travel beyond a
. The four energies of interest
are: 10 meV, 1 meV, 100 keV, and 10 keV. This covers the energy range
relevant to energetic particle detectors on the Pioneer, Voyager, and Galileo
spacecraft. The effect of injection radius, demonstrated qualitatively for
10 meV particles in Fig. 6, is tested quantitatively by limiting injection to
a single radius and varying that radius in subsequent runs. For each
injection radius, four separate simulations are executed, one for each of the
aforementioned energies. The number of particles that travel beyond a 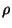 boundary of
boundary of 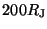 in a constant time are considered to ``escape'' the
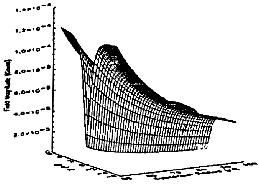
magnetodisc. Figure 7 shows the fundamental result of this research. The
probability of escape via the
in a constant time are considered to ``escape'' the
magnetodisc. Figure 7 shows the fundamental result of this research. The
probability of escape via the
magnetodisc is clearly
dependent on injection energy and 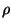 . Once a given particle species is
injected from a certain escape radius as determined by Fig. 7, all particles
of that energy proceed to escape to the predefined boundary. The probability
of escape increases with injection energy and injection
. Once a given particle species is
injected from a certain escape radius as determined by Fig. 7, all particles
of that energy proceed to escape to the predefined boundary. The probability
of escape increases with injection energy and injection 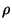 . The error in
the calculations required to establish Fig. 7 is confined to
. The error in
the calculations required to establish Fig. 7 is confined to 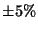 .
.
7. Discussion
We have assumed that particles propagate along the time-independent,
smooth magnetic field in Eqs. (16) and (17). However, naturally
occurring magnetic fields, like those in Jupiter's magnetosphere, fluctuate
on a range of times and scales. These magnetic fluctuations can scatter
charged particles. The pitch angle of a particle can perturbed by Coulomb
collisions, plasma waves, or small-scale field irregularities. Such effects
could cause the particle to ``jump'' to an otherwise restricted region of
phase space and cross boundaries in the Poincare surface of section. A more
accurate simulation model would incorporate pitch angle scattering to account
for such effects as mentioned above. However, Cheng and Decker [1]
demonstrated the ``relative unimportance of scattering, even when the
scattering substantial populates the regular (bounded) orbit region of phase
space''.
The particles in this simulation are treated as test particles, i.e., their
presence does not affect the existing field. As has been shown, these
particles do tend to drift in the direction of the current, so drift motion
will actually augment the current density. Since the contribution of these
particles to the current disc is small, it is reasonable to ignore the self
consistent aspects of the problem.
We have not specified the origin of the injected protons in our simulation.
One possible source is the Jovian ionosphere. The Voyagers discovered active
volcanoes on the moon Io, probably set off by the tidal pumping between
Europa and Ganymede, and Jupiter. The volcanic material is ejected at
approximately 1.05 kilometers/sec, enough to escape the moon. Io appears to
be the principle contributor of matter in the Jovian magnetosphere, secondary
of course to Jupiter. Another contributor of particles may well be from
outside the system, as Goertz et al. [7] predicted the existence of open
field lines.
This research was carried out only for protons. It is well known that
Jupiter's magnetotail contains high abundances of heavier ions such as oxygen
and sulfur, that evidently originate at Io. The radial escape mechanism will
also apply to these heavier ions. We are currently investigating this radial
loss process for these heavier ions for comparison with spacecraft
measurements. Also, Jupiter's magnetosphere is able to trap highly
relativistic electrons. Our trial simulation of positrons, displayed in
Fig. 6.7, shows clearly that electrons will also undergo nonadiabatic motion
in Jupiter's deep magnetotail. We are also actively investigating the motion
of such relativistic electrons in the Jovian magnetodisc. The results of this
research can also be compared with spacecraft observations of relativistic
electrons.
Acknowledgments
The author is extremely grateful to R.B. Decker for his time, patience,
notes, thoughts, discussion, use of office, use of facilities, and anything
else I forgot. I would also like to thank my parents, teachers, and JHUAPL.
This work was supported by no grants and I received no other assistance.
References
1. A.F. Cheng, R.B. Decker, J. Geophys. Res. 97, 1937 (1992)
2. T.G. Northrop, The Adiabatic Motion of Charged Particles, Wiley,
New York (NY) 1963
3. B.A. Randall, in: The Magnetospheres of Earth and Jupiter,
Ed. V. Formisano, D. Riedel, Dordrecht 1975, p. 353
4. J.A. Van Allen, D.N. Baker, B.A. Randall, D.D. Sentman, J.
Geophys. Res. 79, 3559 (1974)
5. T.G. Northrop, C.K. Goertz, M.F. Thomsen, J. Geophys. Res. 79, 3579 (1974)
6. E.J. Smith, L. Davis, Jr., D.E. Jones, P.J. Coleman, Jr., D.S. Colburn,
P. Dyal, C.P. Sonett, A.M.A. Frandsen, J. Geophys. Res. 79, 3501 (1974)
7. C.K. Goertz, D.E. Jones, B.A. Randall, E.J. Smith, M.F. Thomsen,
J. Geophys. Res. 81, (1976)
8. W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery, Numerical Recipes in C, sec. ed., Press Syndicate of the University of
Cambridge, New York (NY) 1992
9. W.H. Press, S.A. Teukolsky, Comput. Phys. 6, 188 (1992)
10. J. Chen, Palmadesso, J. Geophys. Res. 91, 1499 (1986)
11. J. Buchner, L.M. Zeleny, J. Geophys. Res. 94, 11, 821 (1989)
12. H. Karimabadi, P.L. Pritchett, F.V. Coroniti, J. Geophys. Res. 95, 17, 153 (1990)
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

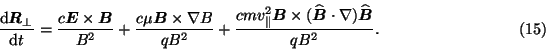
































![\begin{displaymath}\hspace*{-25pt}\frac{\left\vert-M/\rho^3+ab_0C
/\rho^{\alpha...
...rho^{\alpha+1}\!-\! aC/\rho^{\alpha+3}]^2\right\}
^{\frac12}}.\end{displaymath}](img85.gif)











![\includegraphics[width=4.6in]{maj7}](img141.gif)