|
Reconstrution of light intensity
fluctuations from photon-counting data is a typical ill-posed inverse problem
for non-Hermitian transforming operator. Such problems cannot be solved with
the help of eigenfunction representation which diagonalizes the operator and
simplifies the regularization of a quasi-solution. We describe an analytical
method to solve this inverse problem using the Poisson transform operator
representation in a mixed basis which diagonalizes the Poisson transform. On
the base of the proposed method we performed numerical experiments with
typical intensity distributions. We showed that the reconstruction procedure
is stable and may be used even when the level of statistical errors is
relatively high. In conclusion we describe the results of the inversion
procedure in application to the processing of experimental data on photon
counts statistics.
|
1. Introduction
A common problem in the investigation of light fluctuations is to infer the
probability density function of intensity from those of the photon counts. In
the semiclassical approximation these two functions are related through the
Poisson transform [1]. This problem, which is known as an inverse problem of
photon counts statistics has been a subject of extensive studies. It is a
typical ill-posed problem and it has the same features as a well known
problem of blurred and distorted images restoration [2]. Analytical methods
[3, 4] have been demonstrated to work when the corresponding functional
relationship is known. Obviously, these methods are unusable for experimental
data processing. Even small statistical errors cause strong variations in the
resulting estimation of light intensity probability density function (PDF)
when PDF of photon counts is estimated from a measured histogram. Some
methods of numerical solutions of this problem have been proposed [5-9]. One
procedure [5] makes use of the Taylor expansion of the light intensity PDF
characteristic function whose coefficients are given by the photon counts
PDF. Unfortunately, the limited number of values of the photodetected
histogram makes the expression of such expansion valid only in a narrow
region of characteristic function argument and prevents its application for
experimental data processing. Recently, a generalization of this method with
the help of Pade approximation has been proposed [8] and has demonstrated
good results for low level photon rates. The problem there is the selection
of a Pade approximation from the number of acceptable choices, thus
additional physical constraints and consistency with experimental data is
required [9]. Byrne et al. [7] gave a stable numerical procedure of the
intensity PDF estimation by means of Tikhonov regularization [10] which
provides the minimum norm of the solution in the Hilbert space. But as all
such methods, this technique does not permit to estimate the necessary
regularization level and requires additional physical considerations.
Bedard [6] photon counts statistics inverse problem solution is based on the PDF's expansion in terms of the orthogonal Laguerre series. It is a special case of the common input function orthogonal expansion which is the most useful method to solve such problems. This procedure does not permit to determine error in PDF estimation and is not optimized with respect to the Poisson transformation operator, which is its principal disadvantage.
In this work we suggest a new approach to solve the photon counts statistics inverse problem which is based on the optimized PDF's orthogonal expansions and the transform operator representation in a mixed basis. The main advantages of such approach are: (a) maximum simplicity of the solution obtained -- direct and inverse matrices in this representation are diagonal; (b) the possibility to check the regularization level and the estimation errors by simple restriction of eigenvalues taken into account in the inverse matrix; (c) the necessity to accomplish numerical calculations only on analytically defined symmetrical matrices of limited dimensions, which are given by the maximum number of registered photon counts (conventionally it does not exceed 100).
2. Probability distribution of the photoelectrons
Let us briefly consider the relationship between the statistics of the
photoelectron counting and the light falling on it (the direct problem of
photon counting statistics). From the experimental measurements of the
photoelectron counting one can draw conclusions on the statistical properties
of light which in turn have wide applications to various fields of science.
The last problem is the inverse problem of photon counting statistics and it
is the main problem of our consideration.
Consider a beam of light falling on a photoelectric detector. Assume that n photoelectrons are ejected in a certain time interval T. Of course, only the photoelectrons and not the photons are observable and our discussion must therefore be confined to the statistical behavior of the photoelectrons. Although it is tempting to associate the ejection of a photoelectron with the arrival of a photon, this picture becomes inadmissible by the uncertainty principle for time intervals shorter than the inverse frequency band width of light. Restriction to a ``homogeneous'' beam ensures that there are no large phase differences between different parts of the beam.
The fluctuations of the number of particles n therefore have two causes. First, there are fluctuations of the wave intensity I(t), and second, the stochastic fluctuations of particles. This twofold source of the fluctuations results in a departure from classical statistics, as was shown by Mandel [1].
Let P(n,T) denote the probability that n photoelectrons are ejected in a
time interval T. It can be shown in a usual way that under the common
assumptions that P(n,T) is a Poisson distribution in n:
3. Diagonal representation of Poisson transformation in mixed basis
The inverse problem of photoelectron-counting statistics consists in finding
the probability density of integral intensity W from the experimental data
obtained for the probability distribution P(n). Mandel's equation (2) can
be expressed in the functional form as follows:
Effective method of regularization of any inverse problem ![]() gives
the solution expansion in appropriate finite-dimensional orthogonal basis. If
the mapping operator
gives
the solution expansion in appropriate finite-dimensional orthogonal basis. If
the mapping operator ![]() is self-conjugated it is convenient to
choose
its own eigenvectors as such basic functions. The main advantage of this
procedure is the simplicity of quasi-solution retrieval, which is caused by
diagonality of forming operator. Actually, a self-conjugated operator maps
its domain onto itself, and we can use the same system of basic functions,
that is the eigenfunctions of operator
is self-conjugated it is convenient to
choose
its own eigenvectors as such basic functions. The main advantage of this
procedure is the simplicity of quasi-solution retrieval, which is caused by
diagonality of forming operator. Actually, a self-conjugated operator maps
its domain onto itself, and we can use the same system of basic functions,
that is the eigenfunctions of operator ![]() , to represent source and
outlet functions (z and y respectively). In this case decomposition
coefficients of y (ai) and z (bi) are connected by a simple
equation
, to represent source and
outlet functions (z and y respectively). In this case decomposition
coefficients of y (ai) and z (bi) are connected by a simple
equation
Unfortunately, this method cannot be used directly when
![]() .
In particular, a class of such problems is formed by all inverse problems in
which the set of values of operator
.
In particular, a class of such problems is formed by all inverse problems in
which the set of values of operator ![]() does not coincide with its
domain, so that {y} and {z} sets are different. A typical problem of
this class is the inverse problem of photoelectron-counting statistics. In
fact, the operator
does not coincide with its
domain, so that {y} and {z} sets are different. A typical problem of
this class is the inverse problem of photoelectron-counting statistics. In
fact, the operator ![]() in Eq. (3) maps the set of integrable positive
functions P0(x) on the set of infinite-dimensional vectors P(n), which
are defined on the integer variable
in Eq. (3) maps the set of integrable positive
functions P0(x) on the set of infinite-dimensional vectors P(n), which
are defined on the integer variable ![]() To solve such problem we
propose to use mixed representation of the operator
To solve such problem we
propose to use mixed representation of the operator ![]() in a basis,
which has the main feature of a self-conjugated operator in its own
representation -- the diagonality of corresponding matrix. This
representation preserves all advantages of eigenrepresentation in inverse
problem regularization but the class of solvable problems is substantially
longer. Indeed, Eq. (4) which relates the coefficients of the orthogonal
decomposition of P0(x) and P(n) in corresponding spaces is still valid
if the basic functions are defined by the equation,
in a basis,
which has the main feature of a self-conjugated operator in its own
representation -- the diagonality of corresponding matrix. This
representation preserves all advantages of eigenrepresentation in inverse
problem regularization but the class of solvable problems is substantially
longer. Indeed, Eq. (4) which relates the coefficients of the orthogonal
decomposition of P0(x) and P(n) in corresponding spaces is still valid
if the basic functions are defined by the equation,
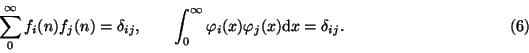
At first, we have to point out an essential refinement of the transformation
(3) formal definition. To determine the problem with the required
mathematical accuracy, let us define the domains of P0(x) and P(n) as
finite intervals in x and n spaces, respectively, so that
Now it is easy to verify that Eqs. (5), (6) are satisfied if functions
![]() and vectors fi(n) are the solutions of the following
equations:
and vectors fi(n) are the solutions of the following
equations:

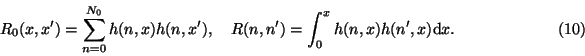
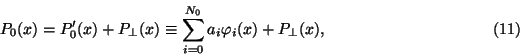
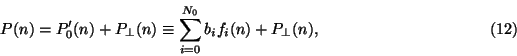
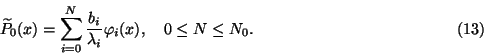

4. Error estimation
The question of principal importance in every method of the inverse problem
solving is error estimation in the reconstructed probability density. As it
follows from the solution structure, there are three main kinds of errors:
1) a systematic error Pc(x) caused by the projection of P0(x) onto the
subspace which is orthogonal to the subspace of quasi-solutions P0(x):
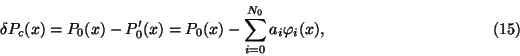
2) a systematic error PN of the projection of P0(x) onto the subspace
of regularized quasi-solutions with the dimensionality N<N0:
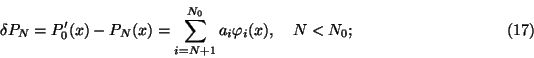
3) finally, a random error PE which is due to the statistical fluctuations
of the input data in the measured histogram
![]() .
.
A quantitative estimation of the first type errors is rather complicated. We
can use the following consideration. As it can be shown, every residual
Pc(x) is mapped by the operator L on a subspace which is orthogonal to
the measured functions P'(n) until n<N0, and therefore we can determine
Pc (x) only from the data for n>N0. Because of the assumption that
P(n)=0 for all n>N0, the statistical error in this region is too large
and no reasonable estimations can be obtained. It means that this error is
independent of the regularization method and it can be eliminated only by a
significant increase in data accuracy in the asymptotical limit. With data
sample of limited size it is practically impossible. As it will be shown
below, this error is sufficiently small except in extremely adverse cases,
for example when P0(x) has singularities. If P0(x) is known, the norm
of such type error can be found
![\begin{displaymath}\varepsilon_c^2=\Vert\delta P_c\Vert^2=\int
_0^x[P_0-P'_0]^2...
...^x P_0^2(x){\rm d}x-\sum_{i=0}^{N_0}\vert a_i\vert^2
\eqno(18)\end{displaymath}](img45.gif)
The norm, N, of the finite-dimensional approximation PN(x) error equals
the remainder of the sum in P'0(x):
![\begin{displaymath}\varepsilon_N^2=\int_0^x[P'_0(x)-P_N
(x)]^2{\rm d}x=\sum_{i=N+1}^{N_0}\vert a_i\vert^2.\eqno(19)\end{displaymath}](img46.gif)
Finally, to estimate the norm of random error let us assume that
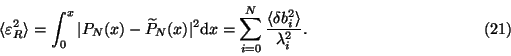
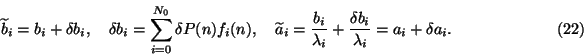
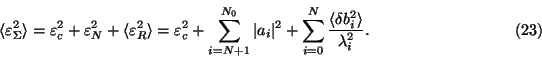
5. Computer simulation
In this section we discuss some typical models of light intensity statistics
and show the results of their PDF's numerical restoration from the computer
simulated histograms of photon counts.
5.1.. Bose-Einstein distribution
If polarized single mode laser light is scattered by a rough moving surface
it can be predicted that the complex amplitude distribution is Gaussian, and
so the distribution of intensity I(t,s) is geometrical (exponential) [13].
If it is assumed that the detector area is much smaller than the average size
of speckle spot and the counting time T is much smaller than the light
coherence time, the integrated intensity distribution is
We performed the computer experiments on numerical reconstruction of
distribution (24) from
![]() data under various conditions. The
histogram was generated with the help of random trial scheme, the size of
sample M was 105 or 106. All experimental data were obtained for the
parameters
data under various conditions. The
histogram was generated with the help of random trial scheme, the size of
sample M was 105 or 106. All experimental data were obtained for the
parameters
![]() . The number of photon counts
n was accumulated in the frequency histogram
. The number of photon counts
n was accumulated in the frequency histogram
![]() . The norm of
error P(n) averaged over 5 histograms was
5.12 x 10-3 for M=105
and
1.91 x 10-3 for M=106.
. The norm of
error P(n) averaged over 5 histograms was
5.12 x 10-3 for M=105
and
1.91 x 10-3 for M=106.
The typical results of PDF reconstruction are shown in Figs. 1 and 2. As can
be seen from Fig. 1, essentially exact solution is obtained for very small
values of N. The influence of random errors in this region is
insignificant, and the resulting error is nearly equal to the projected one.
Figure 2 shows the error norm as the function of the projection
dimensionality N averaged over 5 realizations of histogram. The value of
error for the exact data is shown too. The fluctuation error grows rapidly
with N and becomes leading at N=5. It should be noted that the systematic
error
![]() in this case is extremely small
in this case is extremely small
![]() for N=20), and thus may not be considered. Such
rapid divergence of the series (11) follows from the fact that the
eigenfunction P0(x) has the exponential form which matches the
distribution (24). If the convergence of the series (11) is slower, the
influence of systematic error
for N=20), and thus may not be considered. Such
rapid divergence of the series (11) follows from the fact that the
eigenfunction P0(x) has the exponential form which matches the
distribution (24). If the convergence of the series (11) is slower, the
influence of systematic error
![]() is greater, and in some cases
it becomes the main factor determining the accuracy.
is greater, and in some cases
it becomes the main factor determining the accuracy.
![\includegraphics[width=9cm]{kur1}](img68.gif)
![\includegraphics[width=9cm]{kur2}](img70.gif)
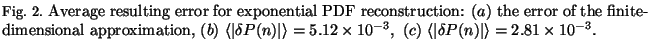
5.2.. Log-normal distribution
The next example corresponds to the physical model of coherent radiation
propagating in a turbulent atmosphere. Prevailing number of experimental data
indicates that the intensity fluctuation distribution in this case obeys the
log-normal law [14]:
![\begin{displaymath}P_0(x)=\frac1{2\sqrt{2\pi}\sigma_\chi\langle x\rangle}
\exp\...
...\rangle}+2\sigma_
\chi^2\right)^2\right],\quad x\ge0.\eqno(26)\end{displaymath}](img72.gif)
We obtained the except distribution P(n) for log-normal fluctuations by
direct numerical calculations of transform (3) for intensity PDF (26). Then
the imitation of experimental histogram was found by means of random term P(
n) which was added to exact P(n). (If the result was negative, we took
![]() .) The norm of random value P(n) was taken
2.5 x 10-3
which corresponded to M=105. The results obtained for the inverse problem
are shown in Figs. 3 and 4. It can be seen that
.) The norm of random value P(n) was taken
2.5 x 10-3
which corresponded to M=105. The results obtained for the inverse problem
are shown in Figs. 3 and 4. It can be seen that
![\includegraphics[width=8.5cm]{kur3}](img76.gif)
![\includegraphics[width=8.5cm]{kur4}](img78.gif)
6. Experimental results
We used the method discussed above to determine the intensity PDF for
experimental data received for two partially polarized superposed light beams
which were scattered by a diffuse surface. As it was shown earlier [15] this
model permits to generate the variety of light intensity distributions and so
it is convenient in testing other experiments. The experimental setup and the
details of experimental procedure are described in [15].
The results of intensity PDF reconstruction are separated in two groups. The
first deals with two-mode radiation with independent intensity fluctuations,
the second corresponds to modes with partially correlated phases
(non-stationary interference). Theoretical expressions for these cases can be
approximately given in the form
![\includegraphics[width=8.5cm]{kur5}](img83.gif)
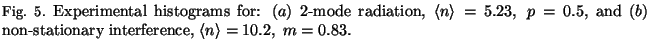
![\includegraphics[width=8.5cm]{kur6}](img85.gif)
![\includegraphics[width=8.5cm]{kur7}](img87.gif)
7. Conclusion
The method presented here can be used in the studies of low intensity optical
fields. The results of computer simulation and experimental data processing
show that the inversion procedure is easy in realization and it has the
necessary stability with respect to numerical calculation errors and input
data statistical fluctuations. Its advantage is also the
possibility of checking the regularization level in estimation resulted. The
restriction of matrix R(n,n') dimension by a finite number N0 of input
photoelectrons enables to eliminate data in the range of large values of
registered counts. This permits to minimize the statistical errors and the
influence of photodetector dead time effects which are of great importance
for high rate photoelectron flow. It should be mentioned also that the
estimations of the solution obtained are continuous functions of the argument
x in spite of the fact that the initial data are discrete and the inversion
is performed in finite-dimensional space.
Acknowledgment
Author wishes to thank Prof. Claude Aime (Univ. of Nice-Sophia Antipolis) for
helpful discussion.
References
1. L. Mandel, in: Progress in Optics, Vol. 2, Ed. E. Wolf, North-Holland, Amsterdam 1963, p. 181
2. R.H.T. Bates, M.J. McDonnell, Image Restoration and Reconstruction, Clarendon Press, Oxford 1986
3. E. Wolf, C.L. Mehta, Phys. Rev. Lett. 13, 705 (1964)
4. B. Saleh, Photoelectron Statistics, Springer Verlag, Berlin 1978
5. J. Perina, Coherence of Light, Van Nostrand, New York 1972
6. G. Bedard, J. Opt. Soc. Am. A 57, 1201 (1967)
7. C.L. Byrne, B.M. Levine, J.C. Dainty, J. Opt. Soc. Am. A 1, 1132 (1984)
8. F. Sultani, C. Aime, H. Lantéri, Pure Appl. Opt. 4, 89 (1995)
9. F. Sultani, C. Aime, H. Lantéri, SPIE Proc. 2647, 2691 (1995)
10. A.N. Tikhonov, V.Y. Arsenin, Solutions of Ill-posed Problems, Halsted Press, Washington 1977
11. C.L. Mehta, in: Progress in Optics, Vol. 8, Ed. E. Wolf, North-Holland, Amsterdam 1970, p. 373
12. F. Riesz, B. Sz.-Nagy, Leçons d'analyse fonctionnelle, Akademiai Kiado, Budapest 1972
13. J.W. Goodman, in: Laser Speckle and Related Phenomena, Ed. J.C. Dainty, Springer Verlag, Berlin 1975, p. 8
14. Laser Beam Propagation in the Atmosphere, Ed. J.W. Strohben, Springer Verlag, Berlin 1978
15. O.I. Barchuk, V.N. Kurashov, A.I. Maschenko, A.T. Mirzaev, Ukr. J. Phys. 33, 1145 (1988)