$^{\strut}$This paper was awarded in the III International Competition (1994/95) "First Step to Nobel Prize in Physics" and published in the competition proceedings (Acta Phys. Pol. A 89 Supplement, S-21 (1996)). The paper is reproduced here due to kind agreement of the Editorial Board of "Acta Physica Polonica A".$_{\strut}$

SUPERLUMINAL PULSE TUNNELING

M. Müller
Gymnasium Münchenstein, Grellingerstrasse 5, 4142 Münchenstein, Switzerland

The quantitative aspects of the tunneling of a Gaussian pulse through a barrier are discussed. The salient features are: the tunneling speed is generally greater than the vacuum speed of light. However causality is not violated. The tunneling time does not depend on the thickness of the forbidden zone. A lateral displacement of the transmitted pulse is observed as is known from total reflexion. The propagation vector of the transmitted pulse deviates from that of the incident pulse.
PACS numbers: 42.25.Bs, 42.25.Gy, 42.65.Re

1. Introduction

The velocity of a light pulse in a dielectric medium without dispersion is given by the speed of light in that medium. However, at the boundaries of such media some interesting effects occur especially under conditions of total reflection. If the boundary at which total reflection occurs does not represent an infinitely extended barrier, partial tunneling through the barrier takes place. Experiments with multilayered mirrors and other barriers [1] which reflect almost all the light have shown that transmission of light appears to occur at superluminal speeds and that transmission speeds do not depend on the thickness of the barrier.

In this paper we discuss the effects for a special kind of barrier which is hit by a Gaussian pulse.

2. The arrangement of the barrier

As a barrier we define a slab of vacuum which separates two dielectric media with a given refractive index n>1. The critical angle of incidence is given by

$$\sin\alpha=\frac{1}{n}.\eqno(1)$$

Light pulses with an angle of incidence greater than this critical angle are almost completely reflected. However, there is a part of the electromagnetic field which can tunnel through the slab if its thickness is of the order of magnitude of the average wavelength of the pulse. It is this transmitted part of the pulse which we are interested in. Figure 1 outlines the arrangement of the boundary for the incoming pulse, resulting in a reflected and transmitted component.

Fig.1. The arrangement of the slab.

3. The description of the pulse

For the sake of simplicity we take a Gaussian pulse as can be provided by a mode-locked laser. For our investigation we define a two-dimensional coordinate system in the plane of incidence (the x,z-plane in Fig. 1). Let us first introduce the two unit vectors $\vec{e}_1$ and $\vec{e}_2$; $\vec{e}_1$ being parallel to the propagation direction of the pulse, $\vec{e}_2$ being perpendicular to $\vec{e}_1$. With the angle of incidence $\varphi_0$ we obtain

$$\vec{e}_1=\left(\begin{array}{c} \sin\varphi_0\\ \cos\varph... ...-\cos\varphi_0\\ \quad\sin\varphi_0\end{array}\right).\eqno(2)$$

The frequency of the laser is $\omega_0$, which leads to the wave vector

$$\vec{k}_0=k_0\vec{e}_1=\frac{\omega_0n}{c}\vec{e}_1. \eqno(3)$$

We choose the coordinate system in such a way that, at the time t=0, the pulse maximum is located at the origin, i.e., the electric field at t=0 is given by

$$E(\vec{r}=a\vec{e}_1+b\vec{e}_2,t=0)=E_0\exp\left[-\frac{1}{2... ...ht)^2\right]\exp\left(-{\rm i}\vec{k}_0\vec{r}\right), \eqno(4)$$

where w is half the pulse width at the point where the field magnitude decreases to $1/\sqrt{\rm e}$, and d is the length of the pulse. The duration of the pulse is given by the relation

$$T=\frac{2dn}{c}. \eqno(5)$$

In Eq. (4) the phase of the electric field at a specific point is determined by $\vec{k}_0$. The field magnitude is a Gaussian distribution with the parameters w and d. The Fourier transform of (4) yields

$$E(\vec{r},t=0)=\frac{wdE_0}{2\pi}\int_{-\infty}^{+\infty}\int... ...es\exp [-{\rm i}\vec{k}(j,m)\vec{r}]{\rm d}j{\rm d}m, \eqno(6)$$

where

$$\vec{k}(j,m)=\vec{k}_0+j\vec{e}_1+m\vec{e}_2. \eqno(7)$$

The integral (6) is the superposition of plane waves which propagate in time. Thus, the complete description of the pulse in time and space is obtained as

$$E(\vec{r},t)=\frac{wdE_0}{2\pi}\int_{-\infty}^{+\infty}\int_{... ...ega(j,m)t-{\rm i}\vec{k}(j,m)\vec{r}]{\rm d}j{\rm d}m, \eqno(8)$$

where

$$\omega(j,m)=\frac{\left\vert\vec{k}(j,m)\right\vert c}{n}. \eqno(9)$$

The Fourier transform (8) of the pulse allows us to calculate for each plane wave the corresponding reflected and transmitted waves and to integrate the contributions of all wave vectors.

4. A plane wave at the barrier

We will now investigate what happens to a plane wave which hits the barrier. $\vec{k}$ denotes the wave vector, $\varphi$ is the angle of incidence. The plane wave can be written in the form

$$E(\vec{r},t)=E\exp({\rm i}\omega t-{\rm i}\vec{kr})=E\exp[{\rm i}\omega t-{\rm i}k(x\sin\varphi+z\cos\varphi)]. \eqno(10)$$

According to Snellius' law the angle of refraction $\psi$ of the wave transmitted into the vacuum slab is

$$\sin\psi=n\sin\varphi. \eqno(11)$$

This angle is only real as long as $\varphi$ is smaller than the critical angle (1). The transmitted wave is described by

$$T(\vec{r},t)=T\exp\left\{-{\rm i}\frac{k}{n}[x\sin\psi+(z-z_{\rm s})\cos\psi]\right\}, \eqno(12)$$

where $z=z_{\rm s}$ is the position of the boundary. The wave vector is $k=\frac{2\pi}{\lambda}=\frac{2\pi}{\lambda_nn}=\frac{k_n}{n}$. The coefficient T is given by Fresnel's formulae

$$T_{\rm p}=\frac{2\sin\psi\cos\varphi}{\sin\varphi\cos\varphi+\sin\psi\cos\psi} E_{\rm p}(x=0,z=z_{\rm s},t),$$

$$T_{\rm s}=\frac{2\sin\psi\cos\varphi}{\sin\varphi\cos\psi+\sin\psi\cos\varphi} E_{\rm s}(x=0,z=z_{\rm s},t), \eqno(13)$$

where the indices p and s indicate the polarization of the electric field parallel and perpendicular, respectively, to the plane of incidence. E is the electric field at the boundary. The formulae (11) and (13) can be derived directly from the Maxwell equations and are therefore also valid for complex values of $\psi$.

Let us examine what the evanescent wave looks like if the angle of incidence $\varphi$ is greater than the critical angle. We use (11) to get an expression for $\cos\psi$

$$\cos\psi=\sqrt{1-\sin^2\psi}=\sqrt{1-n^2\sin^2\varphi}=\pm{\rm i}\sqrt{n^2 \sin^2 \varphi-1}. \eqno(14)$$

For the transmitted wave (12), we then obtain

$$T(\vec{r},t)=T\exp\left[-{\rm i}kx\sin\varphi-\frac{k}{n}(z-z_{\rm s})\sqrt{n^2\sin^2\varphi-1}\right], \eqno(15)$$

where we have chosen the negative sign in (14) because otherwise the amplitude of the transmitted wave would increase exponentially. As we can see, the electric field in the slab is an evanescent wave which propagates parallel to the x-axis. The amplitude of the wave decreases exponentially with the depth $z-z_{\rm s}$. In fact, the evanescent field is partially reflected at the second boundary of the slab and again at the first boundary, so that there is a superposition of multiple reflected waves in the slab. However, we can neglect the parts of the transmitted wave which are reflected several times in the slab before they leave it. For each time the ``wave'' in the slab travels back and forth, its amplitude decreases by the factor $\exp\left(-2l\frac{k}{n}\sqrt{n^2\sin^2\varphi-1}\right)$ (l denotes the thickness of the slab). This value is much smaller than 1 unless the slab is thinner than a small multiple of the average wavelength of the pulse or the angle of incidence is almost equal to the critical angle. However, we want to study the tunneling effect under conditions of almost total reflection. Thus, we exclude extremely thin slabs and angles of incidence close to the critical angle.

The evanescent wave in the slab produces a transmitted wave at the second boundary

$$T'(\vec{r},t)=T'\exp\left\{-{\rm i}k[x\sin\varphi+(z-z_{\rm s}-l)\cos\varphi]\right\}. \eqno(16)$$

l is the thickness of the slab. T' is determined by Fresnel's formulae

$$T'_{\rm p}=\frac{2\sin\varphi\cos\psi} {\sin\varphi\cos\varphi+\sin\psi\cos\psi}T_{\rm p}(x=0,z=z_{\rm s}+l,t),$$

$$T'_{\rm s}= \frac{2\sin\varphi\cos\psi} {\sin\varphi\cos\psi+\sin\psi\cos\varphi}T_{\rm s}(x=0,z=z_{\rm s}+l,t). \eqno(17)$$

We will consider only parallel polarized waves. The description of the transmitted wave is obtained from (10), (13), (15), (16) and (17)

$$T'_{\rm p}(\vec{r},t)= \frac{4\sin\psi\cos\varphi\sin\varphi\cos\psi}{(\sin\varphi\cos\varphi+ \sin\psi\cos\psi)^2}E$$

$$\qquad \times \exp\Big\{-{\rm i}kz_{\rm s}\cos\varphi- \fra... ...omega t-{\rm i}k[x\sin\varphi+(z-z_{\rm s}-l)\cos\varphi]\Big\}$$

and with (14)

$$T'_{\rm p}(\vec{r},t)=\frac{-4{\rm i}n\cos\varphi\sqrt{n^2\si... ...{\left(\cos\varphi-{\rm i}n\sqrt{n^2\sin^2\varphi-1}\right)^2}E$$

$$\qquad \times \exp\left\{-\frac{k}{n}l\sqrt{n^2\sin^2\varphi-... ...ga t-{\rm i}k[x\sin\varphi+(z-l)\cos\varphi]\right\}. \eqno(18)$$

If we compare the formulae (18) and (10) for a selected value of x we see that the incoming wave and the transmitted one are not in phase since the amplitude in (18) is complex whereas in (10) it is real. This will be important below.

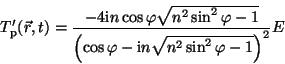
Let us transform the amplitude in (18):

$$\frac{-4{\rm i}n\cos\varphi\sqrt{n^2\sin^2\varphi-1}}{(\cos\v... ...){\rm e}^{{\rm i}[\vartheta(\varphi)-\frac{\pi}{2}]}, \eqno(19)$$

where

$$A(\varphi)=\frac{4n\cos\varphi\sqrt{n^2\sin^2\varphi-1}}{(n^2-1)(n^2\sin^ 2 \varphi-\cos^2\varphi)}$$

and

$$\tan\vartheta(\varphi)/2=\frac{n\sqrt{n^2\sin^2\varphi-1}}{\cos\varphi}. \eqno(20)$$

Finally, we have

$$T'_{\rm p}(\vec{r},t)= A(\varphi)E\exp\Big\{- \frac{k}{n}l\s... ...\left[\vartheta(\varphi)- \frac{\pi}{2}\right]\Big\}. \eqno(21)$$

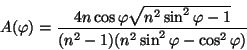
5. The transmitted pulse

Let us return to the Gaussian pulse. In order to obtain the description of the transmitted pulse we have to replace the expressions for the plane waves in (8) by (21)

$$T'_{\rm p}(\vec{r},t)=\frac{wdE_0}{2\pi}\int_{-\infty}^{+\inf... ...\times \exp\left(-\frac{k}{n}l\sqrt{n^2\sin^2\varphi-1}\right)$$

$$\qquad\times\exp\left[{\rm i}\omega t-{\rm i}k[x\sin\varphi+(... ...- \frac{\pi}{2}\right)\right]\Big\}{\rm d}j{\rm d}m. \eqno(22)$$

Fig.2. The components of the wave vectors.

The dependence of $\varphi$ is given by (see Fig. 2)

$$\varphi=\varphi_0+{\rm Arc}\sin\left(\frac{m}{k_0+j}\right)\approx\varphi_0+\frac{m}{k_0}. \eqno(23)$$

It is useful to recall the relations

$$k\sin\varphi=(k_0+j)\sin\varphi_0+m\cos\varphi_0,$$

$$k\cos\varphi=(k_0+j)\cos\varphi_0-m\sin\varphi_0, \eqno(24)$$

which can be obtained from Fig. 2. $\varphi_0$ is the angle of incidence corresponding to $\vec{k}_0$. The main contributions of the integral (22) come from values j and m which are small compared to k₀. For such j and m values the amplitude $A(\varphi)$ in (22) is a slowly changing function of $\varphi$ and can thus be regarded as a constant whose value is determined by the value at $\varphi=\varphi_0.$

$$T'_{\rm p}(\vec{r},t)=\frac{A(\varphi_0)wdE_0}{2\pi} \int_{-... ... $$\qquad\left. -\frac{k}{n}l\sqrt{n^2\sin^2\varphi- 1}\right]$$

$$\qquad\times\exp\left[{\rm i}\omega t-{\rm i}k[x\sin\varphi+(... ...- \frac{\pi}{2}\right)\right]\Big\}{\rm d}j{\rm d}m. \eqno(25)$$

In order to see the influence of the new terms in the exponential function we need the following expansions:

$$k\sqrt{n^2\sin^2\varphi-1}\approx (k_0+j)\sqrt{n^2\sin^2\varp... ...phi_0\cos\varphi_0n^2}{\sqrt{n^2\sin^2\varphi_0-1}}, \eqno(26)$$

$$\vartheta=2{\rm Arc}\tan\left(\frac{n\sqrt{n^2\sin^2\varphi- ... ...sin^2\varphi_0-1}}\frac{m}{\raisebox{-.7mm}{$k_0$}}, \eqno(27)$$

where

$$\vartheta_0=2{\rm Arc}\tan\left(\frac{n\sqrt{n^2\sin^2\varphi_0- 1}}{\cos\varphi_0}\right).$$

Terms of higher order in j and m are neglected. Let us now examine the real and the imaginary exponent in (17) separately.

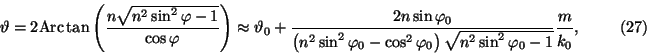
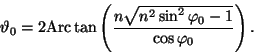
For the real part we get the approximation

$$-\frac{(dj)^2+(wm)^2}{2}-\frac{k}{n}l\sqrt{n^2\sin^2\varphi-1}$$

$$\approx-\frac{(dj)^2+(wm)^2}{2}-\frac{l}{n}(k_0+j)\sqrt{n^2\s... ...c{ml\sin\varphi_0\cos\varphi_0n}{\sqrt{n^2\sin^2\varphi_0- 1}}$$

$$\approx-\frac{d^2(j-j_0)^2+w^2(m-m_0)^2}{2}-l\frac{k_0}{n}\sqrt{n^2\sin^2 \varphi_0-1}+\frac{(dj_0)^2+(wm_0)^2}{2}$$

with

$$j_0=-\frac{l}{d^2n}\sqrt{n^2\sin^2\varphi_0-1}$$

and

$$m_0=-\frac{nl\sin\varphi_0\cos\varphi_0}{w^2\sqrt{n^2\sin^2\varphi_0-1}}. \eqno(28)$$

The imaginary part is obtained as

$${\rm i}\omega t-{\rm i}k\left[x\sin\varphi+(z-l)\cos\varphi\right]+{\rm i}\left[\vartheta(\varphi)-\frac{\pi}{2}\right]$$

$$\approx{\rm i}\omega t-{\rm i}\left\{x\left[(k_0+j)\sin\varph... ...z-l)\left[(k_0+ j )\cos\varphi_0-m\sin\varphi_0\right]\right\}$$

$$\qquad+{\rm i}\left[\vartheta_0+\frac{2n\sin\varphi_0}{(n^2\s... ...sqrt{n^2\sin^2\varphi_0-1}}\frac{m}{k_0} -\frac{\pi}{2}\right]$$

$$={\rm i}\omega t-{\rm i}\left\{(x-\Delta x)[(k_0+j)\sin\varphi_0+m\cos\varphi_0] \right.$$

$$\qquad \left. +(z-l+\Delta z)[(k_0+j)\cos\varphi_0- m\sin\varphi_0]\right\}+{\rm i}\left(\vartheta_0- \frac{\pi}{2}\right)$$

$$\approx {\rm i}\omega t-{\rm i}k\left[(x-\Delta x)\sin\varphi... ...cos\varphi\right]+{\rm i}\left(\vartheta_0-\frac{\pi}{2}\right)$$

with

$$\Delta x=\frac{2n\sin\varphi_0\cos\varphi_0}{k_0(n^2\sin^2\varphi_0- \cos^2\varphi_0 )\sqrt{n^2\sin^2\varphi_0-1}}$$

and

$$\Delta z=\frac{2n\sin^2\varphi_0}{k_0(n^2\sin^2\varphi_0- \cos^2\varphi_0)\sqrt{n^2\sin^2\varphi_0-1}}. \eqno(29)$$

Replacing the above approximations in (25) yields

$$T'_{\rm p}(\vec{r},t)=\frac{BdwE_0}{2\pi}\int_{-\infty}^{+\in... ...infty}\exp\left\{-\frac{d^2(j-j_0)^2+w^2(m- m_0)^2}{2}\right\}$$

$$\qquad \times \exp\left\{{\rm i}\omega t-{\rm i}k[(x-\Delta ... ...i+(z-l+\Delta z)\cos\varphi]\right\}{\rm d}j{\rm d}m \eqno(30)$$

with

$$B=A(\varphi_0)\exp\left[- \frac{(dj_0)^2+(wm_0)^2}{2}- \frac... ...rphi_0-1}+{\rm i}\left(\vartheta_0-\frac{\pi}{2}\right)\right].$$

Introducing the new integration variables

$$j'=j-j_0 \qquad {\rm and}\qquad m'=m-m_0 \eqno(31)$$

transfers (30) into

$$T'_{\rm p}(\vec{r},t)\approx \frac{BdwE_0}{2\pi}\int_{- \inf... ...-\infty}^{+\infty}\exp \left[-\frac{(dj')^2+(wm')^2}{2}\right]$$

$$\qquad\times\exp\left\{{\rm i}\omega t-{\rm i}k[(x-\Delta x)... ...z+\Delta z-l)\cos\varphi]\right\}{\rm d}j'{\rm d}m'. \eqno(32)$$

This is the description of a Gaussian pulse with new parameters. Let us determine them by the two relations

$$k'=k\Rightarrow(k_0+j)^2+m^2=(k'_0+j')^2+m'^2\Rightarrow k'_0\approx k_0+j_0, \eqno(33)$$

$$\qquad k'_0\sin\varphi'_0\approx(k_0+j_0)\sin\varphi'_0=(k_0+j_0)\sin\varphi_0+m_0 ~cos\varphi_0$$

$$\qquad\Rightarrow \varphi'_0\approx\varphi_0+{\rm Arc}\sin\le... ..._0}{k_0+j_0}\right)\approx\varphi_0+\frac{m_0}{k_0}. \eqno(34)$$

The resulting values are only approximations in the first order of m₀ and j₀. However, this is sufficient because these are rather small compared to k₀. The amplitude of the transmitted pulse is smaller by the amount of the factor B. (The phase of B is not relevant for our considerations.) The main direction of the pulse changes by the small angle

$$\Delta\varphi=\frac{m_0}{k_0}=-\frac{nl\sin\varphi_0\cos\varphi_0}{w^2k_0 ~\sqrt{n^2\sin^2\varphi_0-1}}. \eqno(35)$$

The main frequency of the pulse is also slightly modified, i.e. there is a small red shift caused by the tunneling

$$\Delta\omega_0=\Delta k_0\frac{c}{n}=j_0\frac{c}{n}=- \frac{cl}{d^2n^2}\sqrt{n^2\sin^2\varphi_0-1}. \eqno(36)$$

The latter increases with the angle of incidence and the thickness of the slab. The shorter the incoming pulse the greater the frequency shift, the latter depending on the inverse square of the pulse duration.

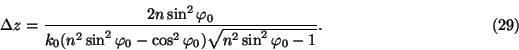
Let us find the maximum of the transmitted Gaussian wave packet at a specific time t. In a homogeneous medium without dispersion the maximum of a Gaussian pulse travels at a constant speed given by the vacuum speed of light divided by the refractive index of the medium. Its amplitude decays with time because of the diffraction of the pulse. After the pulse travelled a distance $\Delta s$, its width can be derived as

$$w(\Delta s)=\sqrt{w^2+\frac{\Delta s^2}{w^2k_0^2}}, \eqno(37)$$

where w denotes the initial width of the pulse. As long as $\Delta s$ is smaller than the so-called Rayleigh range w²k₀, the pulse diffraction is marginal. Beyond this range the width of the pulse increases almost linearly with the propagation distance.

The transmitted wave propagates in the direction of the new wave vector $\vec{k}'_0$. The physical interpretation of this directional change is the following. There are wave components of the incoming pulse that have propagation directions which are more favorable for transmission through the slab than along the main direction of the pulse. These preferentially transmitted components decay less in the slab than the other components of the pulse. These pulse components having the smaller angles of incidence constitute the main part of the transmitted pulse. This explains why the transmitted pulse leaves the slab under an angle slightly smaller than the initial angle of incidence.

Where and when does the transmitted pulse occur on the opposite side of the slab? Equation (32) describes the pulse after transmission through the slab. By way of extrapolation to the time t=0, we may define a virtual origin of the pulse, which is shifted by $x=\Delta x$, $z=l-\Delta z$ with respect to the true origin (x=0, z=0). From this virtual origin and the propagation vector we obtain the exit position ($x_{\rm out}$, $z_{\rm out}=z_{\rm s}+l$) for the transmitted pulse

$$x_{\rm out}=\Delta x+(z_{\rm s}+\Delta z)\tan\varphi'_0\appro... ..._0+\frac{m_0}{k_0\cos^2\varphi_0}\right)+\Delta z\tan\varphi_0$$

$$\qquad=z_{\rm s}\tan\varphi_0-\frac{z_{\rm s}n\tan\varphi_0l}... ...phi_0 -\cos^2\varphi_0)\sqrt{n^2\sin^2\varphi_0-1}}. \eqno(38)$$

The first term is the x-coordinate where the incoming pulse hits the slab. The second term is the shift due to the fact that the transmitted pulse is mostly built up by waves with a smaller angle of incidence than $\varphi_0$. The part of the pulse which propagates in the direction of $\varphi'_0$ reaches the slab earlier and at a smaller value of x than the whole wave packet. Therefore the transmitted pulse leaves the slab at a backward shifted position. The third term is the lateral shift of the Gaussian pulse which is well known from total reflection [2]. This is due to the phase differences between the transmitted and incoming pulse components. In the case of a single slab the lateral displacement of Gaussian pulses is never greater than the width of the pulse. The fact that the second term is proportional to the initial distance, $z_{\rm s}$, of the pulse from the slab is related to the diffraction of the pulse: the longer this distance the larger the spatial separation from the main pulse of those wave components which contribute most to transmission. The time point at which the transmitted pulse leaves the slab is given by

$$t_{\rm out}=\frac{n}{c}\frac{z_{\rm s}+\Delta z}{\cos\varphi... ...{k_0}\right)z_{\rm s}+\frac{n}{c}\frac{\Delta z}{\cos\varphi_0}$$

$$\qquad\approx \frac{z_{\rm s}n}{c\cos\varphi_0}- \frac{n^2l\... ...hi_0 -\cos^2\varphi _ 0)\sqrt{n^2\sin^2\varphi_0-1}}.\eqno(39)$$

The first term denotes the time when the incoming pulse reaches the slab. The second expression is due to the shorter distance which pulse components with a smaller angle of incidence have to travel. The last term, which is rather small, denotes the additional time which is required for the lateral displacement of the pulse. If the pulse is not extremely wide (small w) and if there is a sufficiently long path to the slab, the transmitted pulse appears earlier on the far side of the slab than the incident pulse reaches the barrier.

Let us consider the tunneling time. There are some difficulties to define a tunneling time. Experimentally it is not possible to detect directly the time point when the pulse leaves the slab, but the pulse must be observed somewhere in the adjacent medium behind the slab. The time needed by the pulse to get from its origin to the point of detection can be measured. The question is what we should compare it to. We could do the same experiment without a slab. However, as we have seen the transmitted pulse has a slightly different direction than the original pulse. Thus, an identical but undisturbed pulse will not be detected at the same place as the transmitted pulse. Thus, the two paths of the pulses cannot be directly compared. It is much better to take as reference a pulse which travels through the homogeneous medium with the same direction as the transmitted pulse (see Fig. 3). In this case the two paths are parallel and differ only in the small lateral shift caused by the slab. Let us define the tunneling time as the difference between the time point when the maximum of the transmitted pulse appears on the far side of the slab and the time point when the undisturbed pulse hits the slab. This yields

$$t_{\rm tunnel}=t_{\rm out}-\frac{n}{c}\frac{z_{\rm s}}{\cos\v... ...phi_0 -\cos^2\varphi_0)\sqrt{n^2\sin^2\varphi_0-1}}. \eqno(40)$$

This value is independent of the thickness of the slab!

Fig.3. The arrangement of the experiment to measure the time differences between tunneled and undisturbed pulses.

If we calculate the difference between the time needed by a pulse to reach the detector (Fig. 3) either with or without a slab in between we obtain

$$\Delta t=\frac{n}{c}\Delta s-t_{\rm tunnel}=\frac{n}{c}\left[... ...t}-z_{\rm s}\tan\varphi'_0)\sin\varphi'_0\right]-t_{\rm tunnel}$$

$$\approx\frac{n}{c}\left[l\cos\varphi'_0+\frac{2n\tan\varphi_0... ...{n^2\sin^2\varphi_0-1}}\sin\varphi' _0 \right]-t_{\rm tunnel},$$

$$\Delta t\approx\frac{n}{c}l\cos\varphi'_0. \eqno(41)$$

This result is quite interesting. It shows that the tunneling happens almost instantaneously. The time required for the tunneling corresponds to the time which the evanescent field needs to cover the lateral shift. Had we defined the tunneling time as the difference between the time points of the incoming and outgoing pulse maxima, we would even have obtained a negative value.

The question is whether these results violate causality. Apparently the tunneling time for the pulse maximum is superluminal. However, it must be emphasized that it is only the maximum which appears to travel at this speed. Actually the pulse is reshaped in the slab and comes out in a different form. Furthermore, the energy distribution of Gaussian pulses is not limited in space. Therefore, we cannot apply the principle of causality in its simplest form. Only if there was a distinct front of the pulse one could state that at any point no signal can be detected before the pulse front propagating with the vacuum speed of light would reach it.

6. Visualization of tunneling

Fig.4. Development of a pulse reflected at and transmitted through a barrier.

Fig.5. Development of a pulse reflected at and transmitted through a barrier (viewed along the z-axis).

Fig.6. Development of a pulse reflected at and transmitted through a barrier (viewed along the x-axis).

The following pictures are not based on the above approximations, but take into account multiple pulse reflections. They show the development of a tunneling pulse in time. The first series (Fig. 4) gives an overview: the incident pulse approaches from behind (z<0, x>0). In the first picture (Fig. 4a) the pulse maximum is expected to be still in front of the slab which is located between z=0 and z=3. The z coordinate is scaled in units of vacuum wavelengths of the laser. As the pulse is very close to the slab, parts of the incident and reflected pulse interfere. This causes the disturbances and the high values of the amplitude in the vicinity of the slab. Actually one would find standing waves in front of the slab (z<0); however, this fine structure is not resolved. As can be seen, the field magnitude decreases very rapidly in the slab. The maximum of the transmitted pulse already appears in the second picture (Fig. 4b) when the calculated position of the maximum of the incident pulse has not yet reached the slab. The last two figures (Fig. 4c, d) show the further development. Apart from the transmitted Gaussian pulse we can see a second small pulse. Probably it is due to the multiple reflections or to higher order terms which we did not take into account in our approximations. The following two series (Fig. 5a-d and 6a-d) show the pulse at the same time points, but in views perpendicular to the z-axis and x-axis, respectively. In these views the two main effects related to tunneling are nicely born out. In the series of Fig. 5 the backward shift can be observed, whereas in the series of Fig. 6 the fact that tunneling occurs faster than reflection is evident. The maximum of the transmitted pulse already leaves the slab before the incident pulse hits the slab. In Fig. 6d, the transmitted pulse is farther away from the slab than the reflected one.

Acknowledgment

I would like to thank Prof. J. Mostowski (Polish Academy of Sciences, Warsaw) for introducing me to this problem. I am also very grateful to Dr. Ch. Fattinger (F. Hoffmann-LaRoche Ltd, Basel) for his interest and many helpful comments and discussions.

Bibliography

1

R.Y. Chiao, Phys. Rev. A 48, R34 (1993)

2

T. Tamir, H.L. Bertoni, J. Opt. Soc. Am. 61, 1397 (1971)

This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.