$^{\strut}$This paper was awarded in the III International Competition (1994/95) "First Step to Nobel Prize in Physics" and published in the competition proceedings (Acta Phys. Pol. A 89 Supplement, S-15 (1996)). The paper is reproduced here due to kind agreement of the Editorial Board of "Acta Physica Polonica A".$_{\strut}$

NEW FEATURES
OF RELATIVISTIC PARTICLE SCATTERING

P. Gliwa
77-220 Koczaa 136, Poland

Trajectories of charged relativistic particles in the Coulomb field of force are found. In the nonrelativistic case they are ellipses or hyperbolas. The trajectories for scattering in the relativistic case are also studied in this paper. It is shown that the trajectories make some loops, their number may be unlimited. Kinematics (both nonrelativistic and relativistic) in the momentum representation is presented. Scattering cross-section is calculated and discussed.
PACS numbers: 03.20.+i, 03.30.+p

1. Introduction

The great achievement of the XX century physics was the well-known model of the atom created by Lord Rutherford and Niels Bohr. They assumed that electrons orbit around the nucleus under the influence of the Coulomb force. The continuous trajectories similar to the Kepler orbits were quantized in 1913 by Bohr conditions.

N. Bohr considered nonrelativistic orbits. The generalization to relativistic orbits was done in 1916 by Arnold Sommerfeld. In this way he obtained the shape of trajectories in the form of the well-known ``rosette''.

In this paper we study in some detail properties of the relativistic particle trajectories in the Coulomb field. We pay particular attention to trajectories describing scattering and find some new features of them. Namely we show that trajectories may exhibit loops around the center of force. These loops influence the scattering cross-section.

2. Equation of motion in the Coulomb field

Let us consider the motion of a particle with a mass m and charge e in the Coulomb field of charge Ze. The energy of the particle in the relativistic theory is defined as

$$E=c\sqrt{p^2+m^2c^2}+\alpha/r. \eqno(2.1)$$

The first term of this expression is the kinetic energy, the second is the Coulomb potential, where r is the distance from the center of force and

$$\alpha=Ze^2,\eqno(2.2)$$

Ze -- nuclear and e -- particle charges. For $\alpha<0$, we have attraction; for $\alpha>0$ -- repulsion.

For description of the particle motion in the Coulomb field we also need a momentum. It is a vector with a following length:

$$\vec{p}^2={\vec{L}^2\over r^2}+p_r^2,\eqno(2.3)$$

where $\vec{p}$ -- momentum, p_r -- radial momentum, $\vec{L}$ -- angular momentum. Thus the energy is given by

$$E=c\sqrt{p_r+{\vec{L}^2\over r^2}+m^2c^2}+\alpha/r.\eqno(2.4)$$

Hamilton-Jacobi's equation of motion takes the following form:

$$-{1\over c^2}\left(E-{\alpha\over r}\right)^2+\left({\partial S\over\partial r}\right)^2+{L^2\over r^2}+m^2c^2=0.\eqno(2.5)$$

The solution of this equation is given by

$$S=S_0+\int\sqrt{{1\over c^2}(E-\alpha/r)^2-{L^2\over r^2}-m^2c^2}{\rm d}r.\eqno(2.6)$$

This function gives us all the needed information about the motion of the relativistic particle in the Coulomb field of force. The trajectory of the particle may be obtained from Jacobi's equation [1]

$$\varphi=-{\partial S\over\partial L}.\eqno(2.7)$$

Thus

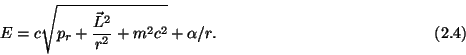
$$\varphi=\varphi_0+L\int{1\over r^2}\left[{1\over c^2}(E-\alpha/r)^2-{L^2\over r^2}-m^2c^2\right]^{-1/2}{\rm d}r. \eqno(2.7a)$$

The dependence $r(\varphi)$, described by this equation, leads to trajectories of different shapes, depending on the relative values of parameters cL and $\vert\alpha\vert$. Let us define

$$\beta =\vert\alpha\vert/cL. \eqno(2.8)$$

(a) If $\beta <1$, then

$$\left( c^2L^2-\alpha^2\right)/r=c\sqrt{(LE)^2-m^2c^2(L^2c^2- \alpha^2)}$$

$$\qquad\times\cos(\varphi\sqrt{1-\alpha^2/c^2L^2})- E\alpha; \eqno(2.8a)$$

(b) for $\beta >1$ we have

$$\left(-c^2L^2+\alpha^2\right)/r=\pm c\sqrt{(LE)^2-m^2c^2(L^2c^2-\alpha^2)}$$

$$\qquad\times \cosh(\varphi\sqrt{\alpha^2/c^2L^2-1})+E\alpha\eqno(2.8b)$$

and finally

(c) for $\beta =1$ we have

$${2E\alpha\over r}=E^2-m^2c^4- \varphi^2\left({E\alpha\over cL}\right)^2. \eqno(2.8c)$$

The difference between the solutions (a) on the one hand and (b), (c) on the other hand consists in the possibility of falling to a center in the two latter cases. Therefore these cases will not be considered further.

The solution (a) may be represented as

$$r={\rho\over\pm1+e\cos(\gamma \varphi)},\eqno(2.9)$$

where, $\pm 1=-\alpha/\vert\alpha\vert$ distinguishes between attraction and repulsion,

$$\rho={L\gamma^2\over\beta E}\qquad {\rm is~a~parameter~of~the~orbit,} \eqno(2.10)$$

$$e={1\over\beta}\sqrt{1- \gamma^2{m^2c^4\over E^2}}\qquad {\rm\mbox{---}~its~eccentricity} ,\eqno(2.11)$$

$$\gamma =\sqrt{1-\beta^2} \qquad {\rm\mbox{---}~a~relativistic~parameter} \eqno(2.12)$$

(for $\beta\ll 1$ these formulas give a nonrelativistic result: $\gamma \approx 1$, $\rho\approx L^2/m\vert\alpha\vert$, $e\approx\sqrt{1+2L^2/m\alpha^2}$).

For e=0 (i.e. $E=mc^2\gamma$) the trajectory is a circle (as in the nonrelativistic theory), but for $e\not= 1$ the trajectories are not the usual conic curves, only somewhat similar to them. In what follows we will consider the case e>1 only, corresponding to particle scattering. The bound states were considered by Arnold Sommerfeld a long time ago. The energy in this case is expressed from (2.11) as

$${E\over mc^2}=\sqrt{{1-\beta^2\over 1-e^2\beta^2}}.\eqno(2.13)$$

This equation gives a very important condition on the eccentricity

$$1<e<{1\over\beta}.\eqno(2.14)$$

In the nonrelativistic kinematics the upper limit goes to infinity and therefore it is always satisfied.

3. Loops

Particles in the Coulomb field move around the center of force. It is usually meant that the particle goes to infinity just after the first interaction with the center (see Fig. 1a).

Fig.1. The particle trajectory: (a) in classical case (hyperbola) for e=1.2 and $\gamma =1$; (b) with one loop for e=1.2 and $\gamma =0.5$; (c) with some loops for e=1.01 and $\gamma =0.2$.

The particles, according to Eq. (2.9), make some rotations -- for example see Fig. 1b. The number of loops depends on the $\gamma$, see Fig. 1c. One should determine how many times the particle circulates around the center. The number of loops may be found as

$$N=\left\vert{\varphi_{\rm as}\over \pi}\right\vert,\eqno(3.1)$$

where $\varphi_{\rm as}$ is the angle between asymptotes of the trajectory (see Eq. 2.8a). Finally,

$$N=\left[{{1\over\gamma}\arccos\left(\mp{1\over e}\right)\over \pi}\right]\eqno(3.2)$$

(the sign - corresponds to attraction and the sign + to repulsion).

The condition (2.14) for e eliminates the loops for the repulsive case, but for attraction N depends on energy and is not limited.

4. Geometry of trajectories

The geometry of relativistic trajectories is very interesting. It depends on the values of E and $\beta$. We will be looking for such values for which one loop exists. The equation N=1 gives us the boundary of the zone containing one loop. From (3.2) for N=1 we get

$${1\over \beta}={\pi\over\sqrt{\pi^2-\arccos(-1/e)}}.\eqno(4.1)$$

This equation with (2.13) gives us the connection between E and $\beta$ after elimination of the eccentricity, see Fig. 2.

Fig.2. The function $f(E/mc^2)=(1/\beta)$ for all values of energy, therefore we can see also the bound states' cases.

5. Scattering cross-section. Attraction

The scattering angle (for attraction or repulsion, depending on the sign of $\alpha$) may be obtained from the equation $\theta=\pi-2\varphi_{\rm as}$, where $\varphi_{\rm as}$ is the angle between asymptotes of the trajectory (see Eq. 2.8a), it is equal to

$$\theta=\pi-{2cL\over\sqrt{c^2L^2-\alpha^2}}\arctan{ v\sqrt{c^2L^2-\alpha^2}\over c\alpha},\eqno(5.1)$$

where v is the velocity of particle at infinity. In a more simple form

$$\theta=\pi-{2\over\gamma}\arctan \left({v\gamma\over c\beta}\right).\eqno(5.2)$$

Scattering cross-section is defined as [2]

$$\left({{\rm d}\sigma\over{\rm d}\Omega}\right)_\theta ={b\ov... ...ta}\left\vert{{\rm d}b\over{\rm d}\theta}\right\vert,\eqno(5.3)$$

where b is the collision parameter. It can be found that

$$L=b p_\infty.\eqno(5.4)$$

The momentum at infinity may be obtained from Eq. (2.1) when $r\rightarrow\infty$, we find

$$b={Lc\over \sqrt{E^2-m^2c^4}}.\eqno(5.5)$$

Now, the scattering angle can be written as

$$\theta=\pi-{2b\sqrt{E^2-m^2c^4}\over\sqrt{b^2(E^2-m^2c^4)-\al... ...^4)-\alpha^2}\sqrt{E^2-m^2c^4}\over\alpha E}\right).\eqno(5.6)$$

Finally, the scattering cross-section calculated from Eq. (5.3) may be written in the parametrized form

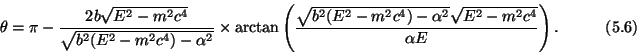
$$\left({{\rm d}\sigma\over{\rm d}\Omega}\right)_\theta={\alpha... ...ver K^2}\xi^2+1\right)-(1+\xi^2) \arctan\xi}\right],\eqno(5.7)$$

where

$$\xi=\tan\left[{(\pi-\theta) \sqrt{b^2K^2-\alpha^2}\over 2bK}\right]\eqno(5.8)$$

and

$$K=\sqrt{E^2/m^2c^4-1}.\eqno(5.9)$$

In the nonrelativistic approximation, i.e. for $\beta\ll 1$ we obtain the Rutherford formula for the cross-section

$$\left({{\rm d}\sigma\over{\rm d}\Omega}\right)_\theta ={\alp... ...E_{\rm K}^2}{1\over\sin^4\left({\theta/2}\right)}, \eqno(5.10)$$

where $E_{\rm K}$ is the nonrelativistic kinematics energy.

6. Numerical examples

The well-known Kepler trajectory is shown in Fig. 3. It was obtained from Eq. (2.9) with $\gamma=1$. In the relativistic case when $\gamma<1$, the form of the trajectory describing a bound state is known as the Sommerfeld rosette -- see Fig. 4. The number of loops depends on the difference of $\gamma$ from 1.

Fig.3. Kepler trajectory e=0.8, $\gamma=1$.

Fig.4. In the relativistic case, $\gamma<1$, the form of the trajectory describing a bound state is known as the Sommerfeld rosette. In this case e=0.8, $\gamma=0.3$.

For the scattering in the attractive case we have the loops, as illustrated in Fig. 1c.

Acknowledgments

It is a great pleasure to thank prof. Yakov Granovskii for useful discussions and for his critical reading of the manuscript.

Bibliography

1

L.D. Landau, E.M. Lifszyc, Teoria pola, PWN, Warszawa 1979, p. 467 (in Polish)

2

T. Mayer-Kuckuk, Fizyka jadrowa, PWN, Warszawa 1983, p. 310 (in Polish)

This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.