The apparent solar motion is not uniform and the length of a solar day is not constant throughout a year. The difference between apparent solar time and mean (regular) solar time is called the equation of time. Two well-known features of our solar system lie at the basis of the periodic irregularities in the solar motion. The angular velocity of the earth relative to the sun varies periodically in the course of a year. The plane of the orbit of the earth is inclined with respect to the equatorial plane. Therefore, the angular velocity of the relative motion has to be projected from the ecliptic onto the equatorial plane before incorporating it into the measurement of time. The mathematical expression of the projection factor for ecliptic angular velocities yields an oscillating function with two periods per year. The difference between the extreme values of the equation of time is about half an hour. The response of the equation of time to a variation of its key parameters is analyzed. In order to visualize factors contributing to the equation of time a model has been constructed which accounts for the elliptical orbit of the earth, the periodically changing angular velocity, and the inclined axis of the earth.
PACS numbers: 95.10.Ce
1 Introduction
1.1. The measurement of time
This paper deals with a problem of the astronomical measurement of time. Let us first introduce some basic definitions. The natural unit of time is the rotation of the earth, that is the apparent daily course of the sun. The length of time between two culminations of the sun is called a solar day. The time-system based on this unit is called apparent solar time. By this system, localities on a given meridian always have the same time-readings.
A comparison of a sundial with a mechanical clock shows that the solar day
has a variable length. Therefore, so-called mean solar time is
commonly used. This is based on a unit which is defined as the average of a
solar day. The mean solar time has been fixed in such a way that it does
not deviate too much from the apparent solar time. The deviations between
apparent solar time and mean solar time are described by the equation
of time
1.2 The periodicity in the solar motion
Two well-known features of our solar system are at the basis of the variations in the apparent motion of the sun:
![\includegraphics[width=12cm]{mul1.eps}](img2.gif)
Fig.1. Apparent path of the sun in a geocentric view. At the perihelion, the sun runs faster than at the aphelion. Equal angleson the plane of the ecliptic do not correspond to equal angles
on the equatorial plane. In this figure there is
but
.
2. The variable angular velocity of the earth
2.1. Kepler's laws
Kepler's first law tells us that all planets are moving in elliptical
orbits around the sun, whereby the latter is positioned at one of the two
focal points. Kepler's second law -- the so-called law of areas --
describes the velocity of the planets. The area swept out per time interval
is constant
![]() .
.
Hence, during the time period t the radius vector from the sun to the
earth sweeps out an area of
Let us now derive the angular velocity of the earth as a function of time. The angle covered by the earth after leaving the perihelion is called ``true anomaly'', denoted here with R (see Fig. 2).
![\includegraphics[width=12cm]{mul2.eps}](img9.gif)
Fig.2. Angles R, M and E at a specific time point. The affinity factor between the elliptical orbit and the circle going through the perihelion and the aphelion is given by b/a. As the angular velocity of the ``real earth'' and the``mean earth'' are both constant, the ratio between the two hatched areas is the same as between the areas of the circle and the ellipse, viz., 1:b/a.
Let us imagine a ``mean earth'' which has also a revolution time
T and is running at a constant speed on a circular orbit with the sun at
its centre. This ``mean earth'' would cover an angle, called ``mean
anomaly'' (M), in the same period of time as the true earth covers the
angle R. In Fig. 2, M is drawn from the centre of the ellipse. The
orbit of the ``mean earth'' is the circle through the perihelion and the
aphelion. The ``mean earth'' starts from the perihelion at the same time as
the true earth. Since the angular velocity of the ``mean earth'' is
constant and its revolution lasts one year (T), M satisfies the simple
equation
We get the following relations from Fig. 2
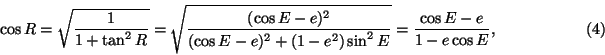
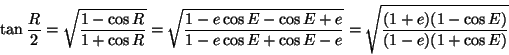
![\begin{displaymath}\qquad ={{\rm i}\over \pi}\oint {\cos\alpha\over \sin^2\alpha...
...}-{1\over \left(z-\cot^2{\alpha \over 2}\right)}\right]{\rm d}z\end{displaymath}](img28.gif)
![\begin{displaymath}\qquad =-{{\rm i}\over 4\pi}\oint\left(z^{n/2}+z^{-n/2}\right...
...eft(z-\cot^2{\alpha \over
2}\right)}\right]{\rm d}z. \eqno(13)\end{displaymath}](img29.gif)
![\begin{displaymath}-{{\rm i} \over4\pi} \left(z^{n/2} +z^{-n/2}
\right) \left[ ...
...y} \left(z\tan^2 {\alpha \over 2}
\right)^i \right]. \eqno(17)\end{displaymath}](img34.gif)
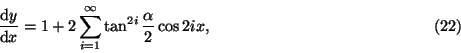


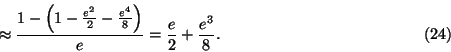
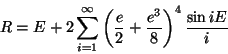
![\includegraphics[width=12cm]{mul3.eps}](img72.gif)
Fig.3. The angular velocity of the earth as a function of time. On average it is aboutper day or
/day =
/day.
3. The inclined plane of the ecliptic
3.1. The earth in space
Since the equation of time is to be examined during a year, the earth can be supposed to always have the same direction in space, i.e., we will not take into account precession and nutation.
We can describe the direction of the axis of the earth with two angles. The
first is the angle between the axis and the norm of the orbit
(![]() ). The second is the angle P formed by the major axis of
the orbit and the projection of the axis of the earth onto the plane
of the orbit (see Fig. 4). At present,
). The second is the angle P formed by the major axis of
the orbit and the projection of the axis of the earth onto the plane
of the orbit (see Fig. 4). At present, ![]() measures about
measures about
![]() , P is about
, P is about ![]() . (P is also the angle which is
covered by the earth between the beginning of winter (21st December) and
the arrival of the earth at perihelion (2nd January).)
. (P is also the angle which is
covered by the earth between the beginning of winter (21st December) and
the arrival of the earth at perihelion (2nd January).)
![\includegraphics[width=12cm]{mul4.eps}](img80.gif)
3.2. The projection of ecliptic angles onto the equatorial plane
The angles which the sun appears to cover relative to the earth are equal
to those the earth actually covers relative to the sun. Since the
corresponding angles parallel to the equatorial plane are needed for the
measurement of time, the ecliptical angles have to be projected onto the
equatorial plane. This results in angle widening or shortening. For an
infinitesimally small angle the projection factor (the deformation factor)
is determined by the angle parameters ![]() and
and ![]() in
Fig. 5, which represents the geocentric view.
in
Fig. 5, which represents the geocentric view. ![]() is measured from
the winter solstice.
is measured from
the winter solstice.
![\includegraphics[width=8cm]{mul5.eps}](img84.gif)
Fig.5. Geocentric view of the projection. In a short time interval, the sun has covered the angle.
is the orthogonal projection of
.
![\includegraphics[width=12cm]{mul6.eps}](img88.gif)
Fig.6. The projection factor as a function of time. The maxima are at the solstices, the minima at the equinoxes.
We get the following relations from Fig. 5:
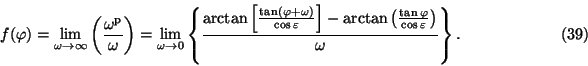
The extremes are situated at the beginning of the seasons. At the summer and winter solstice, the sun reaches, respectively, its highest and lowest position. Here, an ecliptic angle is stretched maximally. At the vernal and autumnal equinox, the sun stands vertically above the equator. Here, ecliptic angles are shortened maximally.
4. The calculation of the equation of time
4.1. Derivation of a more accurate approximation
In order to calculate the equation of time we need the projection of the
true anomaly ![]() as a function of time
as a function of time
![\begin{displaymath}R^{\rm p} = \int\! {\rm d}R^{\rm p} = \int\! f(R\!+\!P) {\rm ...
...arepsilon \over 2} \cos2i(R\!+\!P)
\right]\!{\rm d}R \eqno(41)\end{displaymath}](img99.gif)
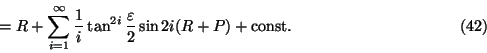

![\includegraphics[width=9cm]{mul7.eps}](img116.gif)
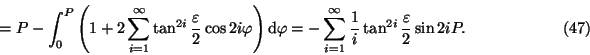
![\includegraphics[width=12cm]{mul8.eps}](img126.gif)
Fig.8. The equation of time with its two main terms. The difference between the maximum in October (min) and the minimum in February (
min) is about half an hour.
Figure 8 shows the equation of time for a whole period of one year. In winter, the value of the equation of time decreases mostly because the angular velocity of the earth and the projection factor reach their maximum. The opposite holds true between the passage through the aphelion and the beginning of autumn. Afterwards, the equation of time itself reaches an extreme value. In the time span between those extrema, especially in summer, the lower angular velocity and the greater projection factor compensate each other.
![\includegraphics[width=9cm]{mul9.eps}](img129.gif)
Figure 9 (taken from [2]) shows the observed phenomenon of the equation of time. In intervals of ten days, a picture of the sky was taken at 8.14 (mean solar time). If the sun moved at a constant speed through the sky, all pictures of the sun would lay on a straight line that would be perpendicular to the daily path of the sun. In winter and in summer, the sun has not reached as far as one would expect (it is below the ``average line'' (2)). Therefore, the value of the equation of time is negative (see Fig. 8). On the other hand, the sun advances faster from April to June and at the end of the year (it is above the ``average line'') and the value of the equation of time is positive. These variations produce the form of a stretched and inclined ``eight'' in the picture.
4.2. The equation of time as a function of its parameters
The equation of time is determined by the following parameters:
1. parameter: the eccentricity. If e=0 a regular variation results that is caused by the inclination of the ecliptic plane. The deviations of the apparent solar time from the mean solar time increase with growing e in winter and autumn. Thus, the yearly variation becomes dominant. Since at the perihelion and aphelion the equation of time is only a function of the ecliptic inclination and the angle P, all plots have the same value at these two points.
2. parameter: the inclination of the ecliptic. ![]() yields a
plot
which is symmetric to the passage through the aphelion. The greater
yields a
plot
which is symmetric to the passage through the aphelion. The greater
![]() the more dominant the variation with a period of half a
year. All plots have four common points at the beginning of each season,
for the equation of time depends only on the two other parameters there
(eccentricity and P). As the projection from the ecliptic plane onto the
equatorial plane does not change the polar angle relative to the winter
solstice,
the more dominant the variation with a period of half a
year. All plots have four common points at the beginning of each season,
for the equation of time depends only on the two other parameters there
(eccentricity and P). As the projection from the ecliptic plane onto the
equatorial plane does not change the polar angle relative to the winter
solstice, ![]() does not influence the value of the equation of
time at the beginning of a season.
does not influence the value of the equation of
time at the beginning of a season.
![\includegraphics[width=12cm]{mul10.eps}](img134.gif)
Fig.10. 1. parameter: the eccentricity. +++ e=0.000,,
,
, x x x e=0.020.
![\includegraphics[width=12cm]{mul11.eps}](img138.gif)
Fig.11. 2. parameter: the inclination of the ecliptic.,
,
,
,
.
![\includegraphics[width=12cm]{mul12.eps}](img144.gif)
Fig.12. 3. parameter: the time interval between the beginning of winter and the passage through the perihelion.days,
days,
days,
days,
days.
3. parameter:
the time interval between the beginning of winter
and the passage through the perihelion.
If ![]() the two main variations vanish both at the beginning of
winter and summer (because winter begins when the earth passes the
perihelion; the aphelion is the summer solstice). Therefore, the resulting
function is symmetric and the extreme values are in autumn and winter. If
the two main variations vanish both at the beginning of
winter and summer (because winter begins when the earth passes the
perihelion; the aphelion is the summer solstice). Therefore, the resulting
function is symmetric and the extreme values are in autumn and winter. If
![]() increases, the two components tend to compensate each other in
winter whereas the negative value in summer begins to dominate.
increases, the two components tend to compensate each other in
winter whereas the negative value in summer begins to dominate.
5. Construction of a model
As one might have some difficulty in imagining the matters treated herein concerning the solar system we decided to construct a model which illustrates the preceding explanations.
5.1. The orbit of the earth
As to the revolution of the earth, the following points have to be taken into account:
A simple solution for this problem is to run a vertical axis (which represents the earth) in an elliptic orbit by two elliptical hollow tracks in parallel planes.
This axis is pushed by a horizontal stick but it is not fixed to it. Thus, the distance between the axis and the rotary centre of the pushing stick can vary. If this stick turns regularly, the speed of the axis in the hollow tracks is not constant; when the distance between the rotary centre and the axis increases, the axis will be pushed at a higher speed.
These considerations serve to find a solution for the second point. We need a higher speed at the perihelion than at the aphelion. Therefore, the rotary centre of the pushing stick has to be placed further away from the perihelion than from the aphelion (see Fig. 13).
![\includegraphics[width=9cm]{mul13.eps}](img152.gif)
5.2. The rotation of the earth
The drive of the rotation of the earth has to be fixed since it will be connected to the revolution drive. On the other hand, the earth (or rather the vertical axis) revolves around the sun. So there has to be a flexible connection between the rotation drive and the axis in the hollow tracks. In our model, we use a chain for this purpose. In order to use the chain always to its entire length we can take advantage of a special feature of the ellipse.
The sum of the distances between the foci and any point on the periphery of the ellipse is constant throughout. If we lead the chain around the foci to the axis in the hollow tracks the chain will always be tight (see Fig. 14).
![\includegraphics[width=7cm]{mul14.eps}](img153.gif)
For the chain of the rotation drive, we have to put one axis into each focus. It will make drive only one of these two axes. Now we have to decide where to place the rotary centre of the revolution drive. In Fig. 14 you can see that it is only possible to place it into the hatched area because otherwise it would interfere with the chain of the rotation drive. Let us put the rotary axis at the most ideal place, that is the focus near the aphelion. There, it also serves as an axis for a sprocket wheel of the chain. The revolution drive being placed in this focus, the rotation drive has to be located in the other focus. (The sprocket wheel at the focus of the revolution drive must not be fixed to the axis because their rotary speeds are not equal.)
Both drives are connected with a transmission that realizes a ratio of approximately 1:300.
5.3. The tilt of the axis of the earth
With a universal joint, we fix a second, tilted axis to the vertical axis
that revolves around the sun. The inclined axis is held in its correct
position (with a tilt of about ![]() ) by a prop, which still allows
the earth to rotate (see Fig. 15).
) by a prop, which still allows
the earth to rotate (see Fig. 15).
![\includegraphics[width=7cm]{mul15.eps}](img155.gif)
![\includegraphics[width=6cm]{mul16.eps}](img157.gif)
The axis of the earth is fixed now with a tilt of about ![]() , but
it is able to swivel round. Figure 16 illustrates how the prop can be
controlled during a revolution so that the special direction of the axis of
the earth is always the same.
, but
it is able to swivel round. Figure 16 illustrates how the prop can be
controlled during a revolution so that the special direction of the axis of
the earth is always the same.
Figure 17 shows the entire model.
![\includegraphics[width=12cm]{mul17.eps}](img159.gif)